Jiexin Duan
Enhanced Nearest Neighbor Classification for Crowdsourcing
Feb 26, 2022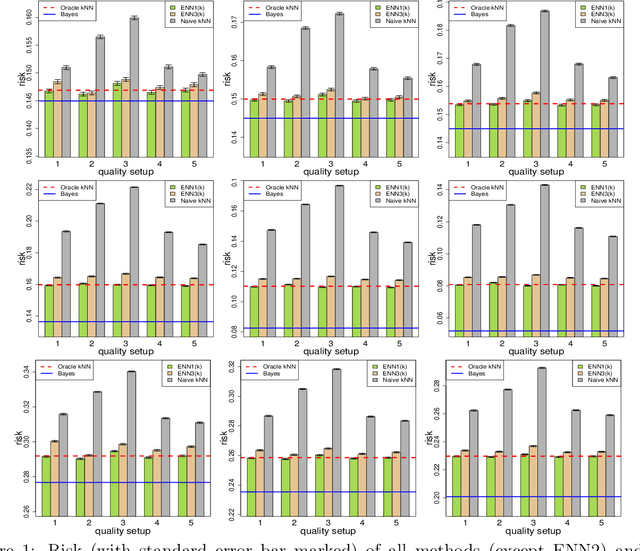
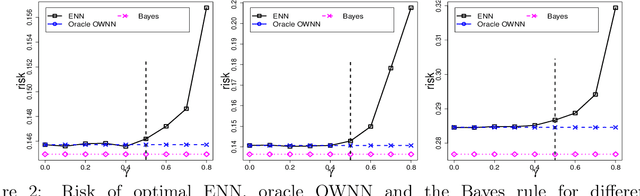
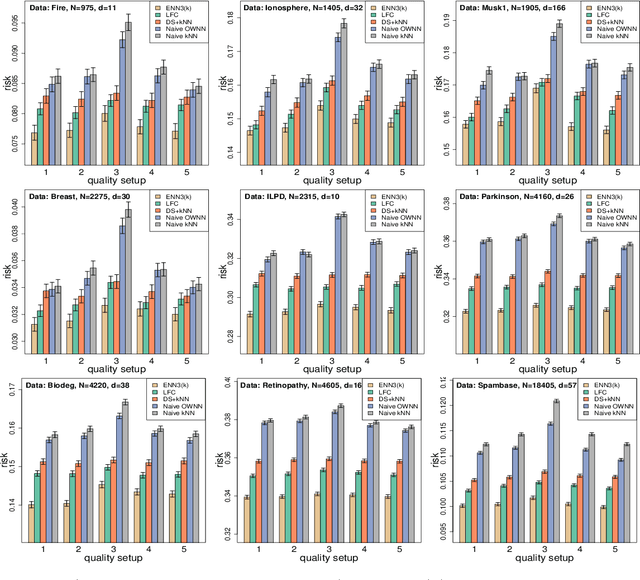
Abstract:In machine learning, crowdsourcing is an economical way to label a large amount of data. However, the noise in the produced labels may deteriorate the accuracy of any classification method applied to the labelled data. We propose an enhanced nearest neighbor classifier (ENN) to overcome this issue. Two algorithms are developed to estimate the worker quality (which is often unknown in practice): one is to construct the estimate based on the denoised worker labels by applying the $k$NN classifier to the expert data; the other is an iterative algorithm that works even without access to the expert data. Other than strong numerical evidence, our proposed methods are proven to achieve the same regret as its oracle version based on high-quality expert data. As a technical by-product, a lower bound on the sample size assigned to each worker to reach the optimal convergence rate of regret is derived.
Rates of Convergence for Large-scale Nearest Neighbor Classification
Sep 03, 2019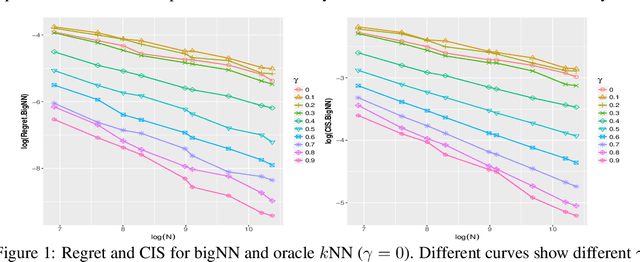
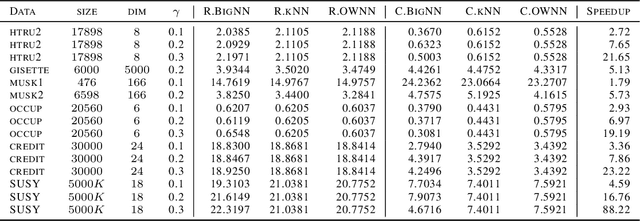
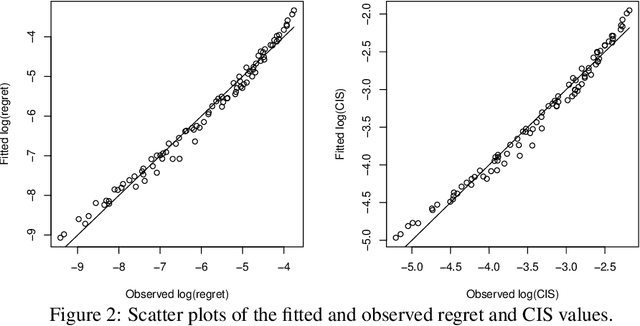
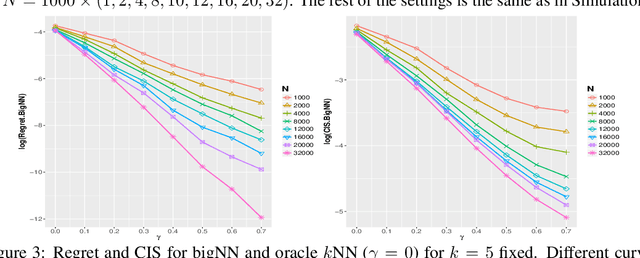
Abstract:Nearest neighbor is a popular class of classification methods with many desirable properties. For a large data set which cannot be loaded into the memory of a single machine due to computation, communication, privacy, or ownership limitations, we consider the divide and conquer scheme: the entire data set is divided into small subsamples, on which nearest neighbor predictions are made, and then a final decision is reached by aggregating the predictions on subsamples by majority voting. We name this method the big Nearest Neighbor (bigNN) classifier, and provide its rates of convergence under minimal assumptions, in terms of both the excess risk and the classification instability, which are proven to be the same rates as the oracle nearest neighbor classifier and cannot be improved. To significantly reduce the prediction time that is required for achieving the optimal rate, we also consider the pre-training acceleration technique applied to the bigNN method, with proven convergence rate. We find that in the distributed setting, the optimal choice of the neighbor k should scale with both the total sample size and the number of partitions, and there is a theoretical upper limit for the latter. Numerical studies have verified the theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge