Non-Oscillatory Pattern Learning for Non-Stationary Signals

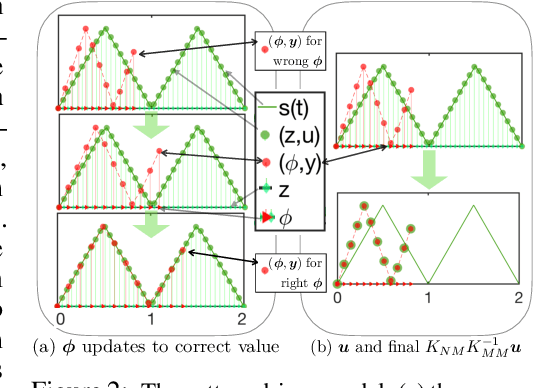
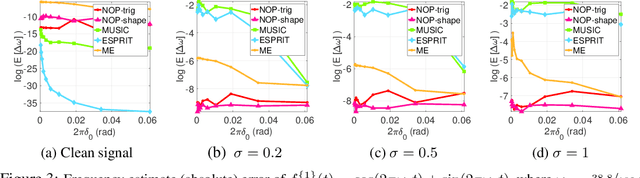
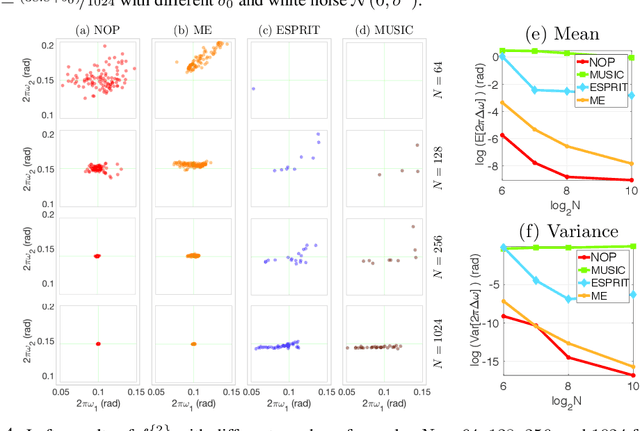
This paper proposes a novel non-oscillatory pattern (NOP) learning scheme for several oscillatory data analysis problems including signal decomposition, super-resolution, and signal sub-sampling. To the best of our knowledge, the proposed NOP is the first algorithm for these problems with fully non-stationary oscillatory data with close and crossover frequencies, and general oscillatory patterns. NOP is capable of handling complicated situations while existing algorithms fail; even in simple cases, e.g., stationary cases with trigonometric patterns, numerical examples show that NOP admits competitive or better performance in terms of accuracy and robustness than several state-of-the-art algorithms.

Recursive Diffeomorphism-Based Regression for Shape Functions

This paper proposes a recursive diffeomorphism based regression method for one-dimensional generalized mode decomposition problem that aims at extracting generalized modes $\alpha_k(t)s_k(2\pi N_k\phi_k(t))$ from their superposition $\sum_{k=1}^K \alpha_k(t)s_k(2\pi N_k\phi_k(t))$. First, a one-dimensional synchrosqueezed transform is applied to estimate instantaneous information, e.g., $\alpha_k(t)$ and $N_k\phi_k(t)$. Second, a novel approach based on diffeomorphisms and nonparametric regression is proposed to estimate wave shape functions $s_k(t)$. These two methods lead to a framework for the generalized mode decomposition problem under a weak well-separation condition. Numerical examples of synthetic and real data are provided to demonstrate the fruitful applications of these methods.