OrionBench: A Benchmark for Chart and Human-Recognizable Object Detection in Infographics

Given the central role of charts in scientific, business, and communication contexts, enhancing the chart understanding capabilities of vision-language models (VLMs) has become increasingly critical. A key limitation of existing VLMs lies in their inaccurate visual grounding of infographic elements, including charts and human-recognizable objects (HROs) such as icons and images. However, chart understanding often requires identifying relevant elements and reasoning over them. To address this limitation, we introduce OrionBench, a benchmark designed to support the development of accurate object detection models for charts and HROs in infographics. It contains 26,250 real and 78,750 synthetic infographics, with over 6.9 million bounding box annotations. These annotations are created by combining the model-in-the-loop and programmatic methods. We demonstrate the usefulness of OrionBench through three applications: 1) constructing a Thinking-with-Boxes scheme to boost the chart understanding performance of VLMs, 2) comparing existing object detection models, and 3) applying the developed detection model to document layout and UI element detection.

Structural-Entropy-Based Sample Selection for Efficient and Effective Learning

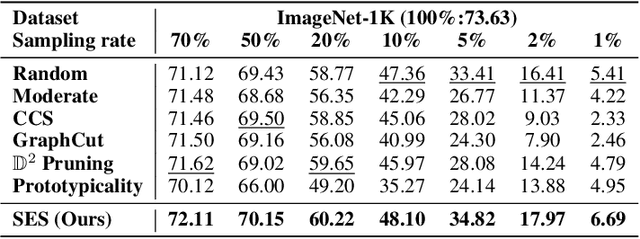
Sample selection improves the efficiency and effectiveness of machine learning models by providing informative and representative samples. Typically, samples can be modeled as a sample graph, where nodes are samples and edges represent their similarities. Most existing methods are based on local information, such as the training difficulty of samples, thereby overlooking global information, such as connectivity patterns. This oversight can result in suboptimal selection because global information is crucial for ensuring that the selected samples well represent the structural properties of the graph. To address this issue, we employ structural entropy to quantify global information and losslessly decompose it from the whole graph to individual nodes using the Shapley value. Based on the decomposition, we present $\textbf{S}$tructural-$\textbf{E}$ntropy-based sample $\textbf{S}$election ($\textbf{SES}$), a method that integrates both global and local information to select informative and representative samples. SES begins by constructing a $k$NN-graph among samples based on their similarities. It then measures sample importance by combining structural entropy (global metric) with training difficulty (local metric). Finally, SES applies importance-biased blue noise sampling to select a set of diverse and representative samples. Comprehensive experiments on three learning scenarios -- supervised learning, active learning, and continual learning -- clearly demonstrate the effectiveness of our method.