Structural-Entropy-Based Sample Selection for Efficient and Effective Learning
Paper and Code
Oct 03, 2024


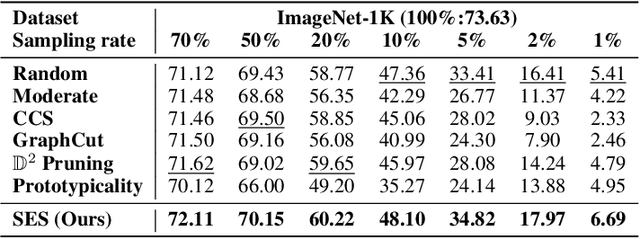
Sample selection improves the efficiency and effectiveness of machine learning models by providing informative and representative samples. Typically, samples can be modeled as a sample graph, where nodes are samples and edges represent their similarities. Most existing methods are based on local information, such as the training difficulty of samples, thereby overlooking global information, such as connectivity patterns. This oversight can result in suboptimal selection because global information is crucial for ensuring that the selected samples well represent the structural properties of the graph. To address this issue, we employ structural entropy to quantify global information and losslessly decompose it from the whole graph to individual nodes using the Shapley value. Based on the decomposition, we present $\textbf{S}$tructural-$\textbf{E}$ntropy-based sample $\textbf{S}$election ($\textbf{SES}$), a method that integrates both global and local information to select informative and representative samples. SES begins by constructing a $k$NN-graph among samples based on their similarities. It then measures sample importance by combining structural entropy (global metric) with training difficulty (local metric). Finally, SES applies importance-biased blue noise sampling to select a set of diverse and representative samples. Comprehensive experiments on three learning scenarios -- supervised learning, active learning, and continual learning -- clearly demonstrate the effectiveness of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge