Byzantine-tolerant distributed learning of finite mixture models

This paper proposes two split-and-conquer (SC) learning estimators for finite mixture models that are tolerant to Byzantine failures. In SC learning, individual machines obtain local estimates, which are then transmitted to a central server for aggregation. During this communication, the server may receive malicious or incorrect information from some local machines, a scenario known as Byzantine failures. While SC learning approaches have been devised to mitigate Byzantine failures in statistical models with Euclidean parameters, developing Byzantine-tolerant methods for finite mixture models with non-Euclidean parameters requires a distinct strategy. Our proposed distance-based methods are hyperparameter tuning free, unlike existing methods, and are resilient to Byzantine failures while achieving high statistical efficiency. We validate the effectiveness of our methods both theoretically and empirically via experiments on simulated and real data from machine learning applications for digit recognition. The code for the experiment can be found at https://github.com/SarahQiong/RobustSCGMM.

Zero-Shot Aspect-Based Sentiment Analysis

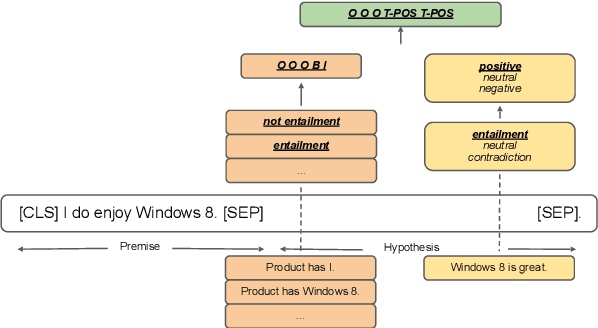
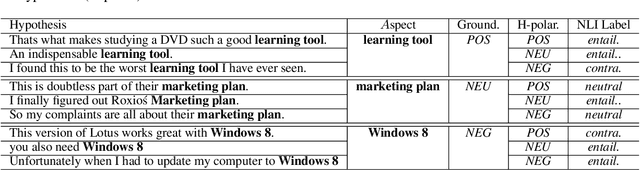
Aspect-based sentiment analysis (ABSA) typically requires in-domain annotated data for supervised training/fine-tuning. It is a big challenge to scale ABSA to a large number of new domains. This paper aims to train a unified model that can perform zero-shot ABSA without using any annotated data for a new domain. We propose a method called contrastive post-training on review Natural Language Inference (CORN). Later ABSA tasks can be cast into NLI for zero-shot transfer. We evaluate CORN on ABSA tasks, ranging from aspect extraction (AE), aspect sentiment classification (ASC), to end-to-end aspect-based sentiment analysis (E2E ABSA), which show ABSA can be conducted without any human annotated ABSA data.

Minimum Wasserstein Distance Estimator under Finite Location-scale Mixtures

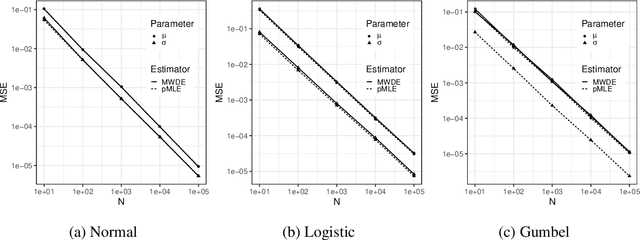
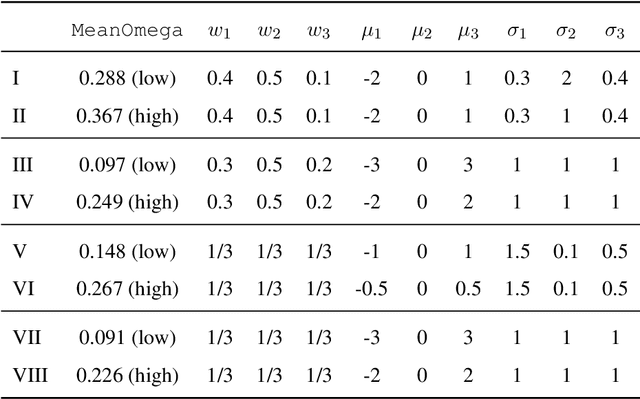
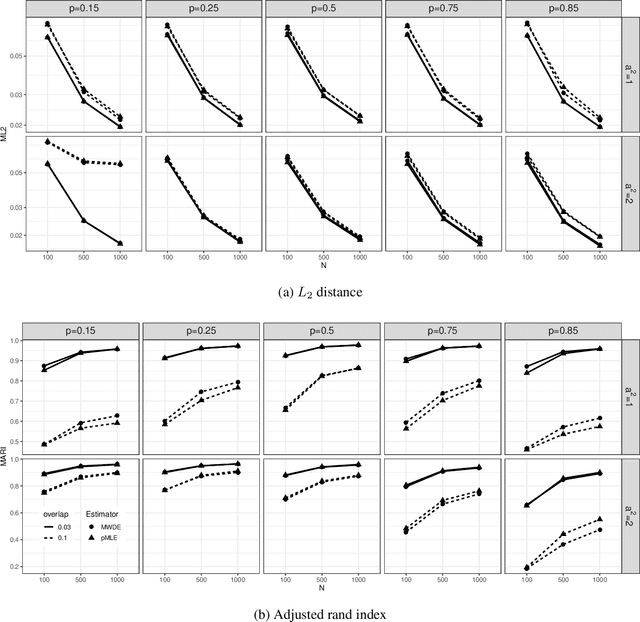
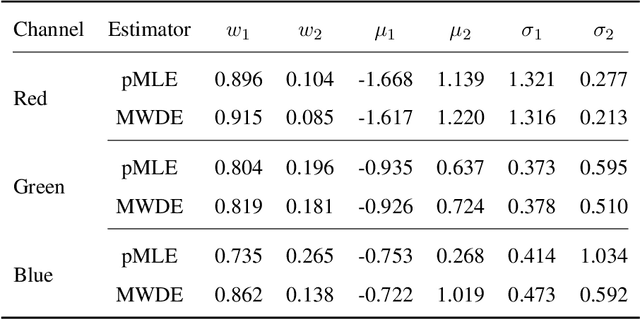
When a population exhibits heterogeneity, we often model it via a finite mixture: decompose it into several different but homogeneous subpopulations. Contemporary practice favors learning the mixtures by maximizing the likelihood for statistical efficiency and the convenient EM-algorithm for numerical computation. Yet the maximum likelihood estimate (MLE) is not well defined for the most widely used finite normal mixture in particular and for finite location-scale mixture in general. We hence investigate feasible alternatives to MLE such as minimum distance estimators. Recently, the Wasserstein distance has drawn increased attention in the machine learning community. It has intuitive geometric interpretation and is successfully employed in many new applications. Do we gain anything by learning finite location-scale mixtures via a minimum Wasserstein distance estimator (MWDE)? This paper investigates this possibility in several respects. We find that the MWDE is consistent and derive a numerical solution under finite location-scale mixtures. We study its robustness against outliers and mild model mis-specifications. Our moderate scaled simulation study shows the MWDE suffers some efficiency loss against a penalized version of MLE in general without noticeable gain in robustness. We reaffirm the general superiority of the likelihood based learning strategies even for the non-regular finite location-scale mixtures.

Distributed Learning of Finite Gaussian Mixtures

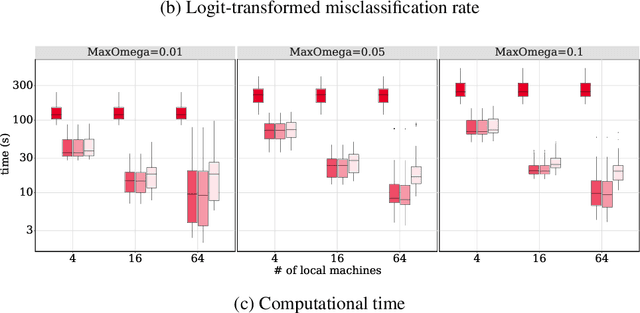
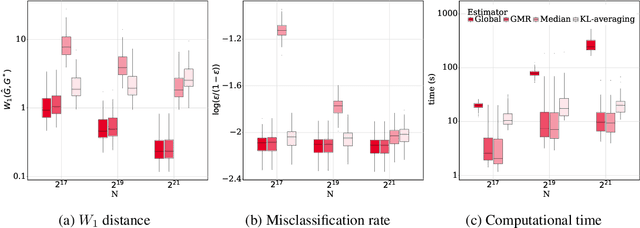
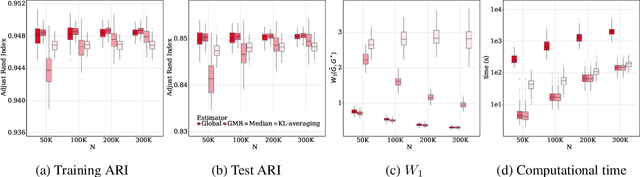
Advances in information technology have led to extremely large datasets that are often kept in different storage centers. Existing statistical methods must be adapted to overcome the resulting computational obstacles while retaining statistical validity and efficiency. Split-and-conquer approaches have been applied in many areas, including quantile processes, regression analysis, principal eigenspaces, and exponential families. We study split-and-conquer approaches for the distributed learning of finite Gaussian mixtures. We recommend a reduction strategy and develop an effective MM algorithm. The new estimator is shown to be consistent and retains root-n consistency under some general conditions. Experiments based on simulated and real-world data show that the proposed split-and-conquer approach has comparable statistical performance with the global estimator based on the full dataset, if the latter is feasible. It can even slightly outperform the global estimator if the model assumption does not match the real-world data. It also has better statistical and computational performance than some existing methods.

A Knowledge-Driven Approach to Classifying Object and Attribute Coreferences in Opinion Mining

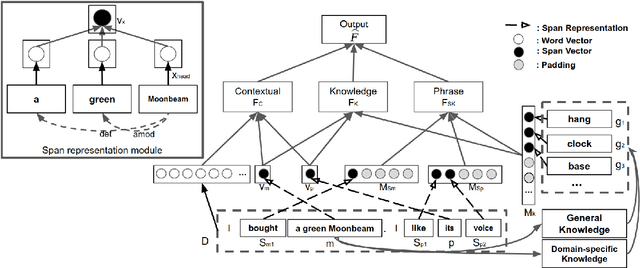
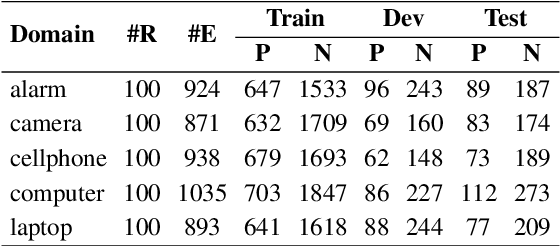
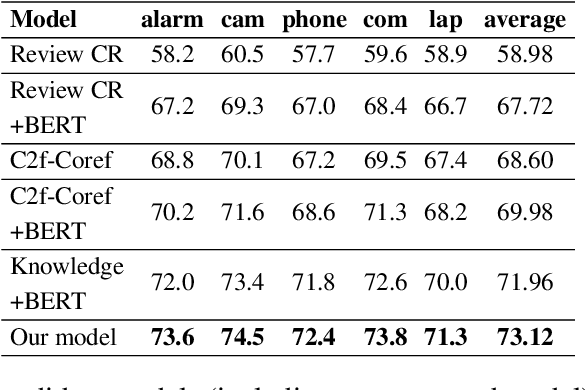
Classifying and resolving coreferences of objects (e.g., product names) and attributes (e.g., product aspects) in opinionated reviews is crucial for improving the opinion mining performance. However, the task is challenging as one often needs to consider domain-specific knowledge (e.g., iPad is a tablet and has aspect resolution) to identify coreferences in opinionated reviews. Also, compiling a handcrafted and curated domain-specific knowledge base for each domain is very time consuming and arduous. This paper proposes an approach to automatically mine and leverage domain-specific knowledge for classifying objects and attribute coreferences. The approach extracts domain-specific knowledge from unlabeled review data and trains a knowledgeaware neural coreference classification model to leverage (useful) domain knowledge together with general commonsense knowledge for the task. Experimental evaluation on realworld datasets involving five domains (product types) shows the effectiveness of the approach.

A Unified Framework for Gaussian Mixture Reduction with Composite Transportation Distance

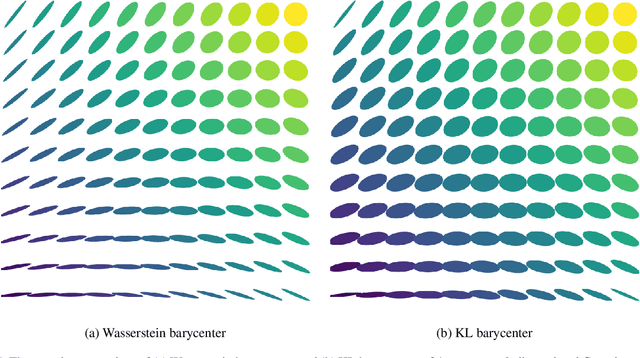
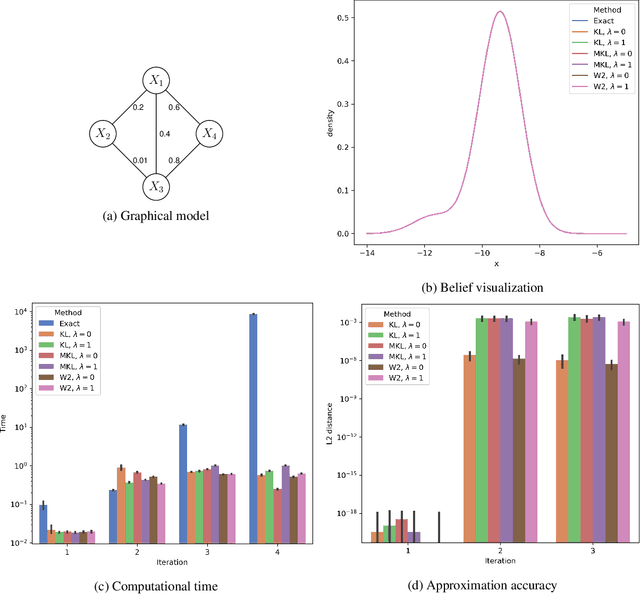
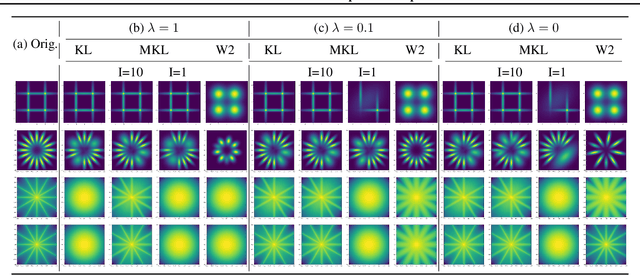
Gaussian mixture reduction (GMR) is the problem of approximating a finite Gaussian mixture by one with fewer components. It is widely used in density estimation, nonparametric belief propagation, and Bayesian recursive filtering. Although optimization and clustering-based algorithms have been proposed for GMR, they are either computationally expensive or lacking in theoretical supports. In this work, we propose to perform GMR by minimizing the entropic regularized composite transportation distance between two mixtures. We show our approach provides a unified framework for GMR that is both interpretable and computationally efficient. Our work also bridges the gap between optimization and clustering-based approaches for GMR. A Majorization-Minimization algorithm is developed for our optimization problem and its theoretical convergence is also established in this paper. Empirical experiments are also conducted to show the effectiveness of GMR. The effect of the choice of transportation cost on the performance of GMR is also investigated.