A Unified Framework for Gaussian Mixture Reduction with Composite Transportation Distance

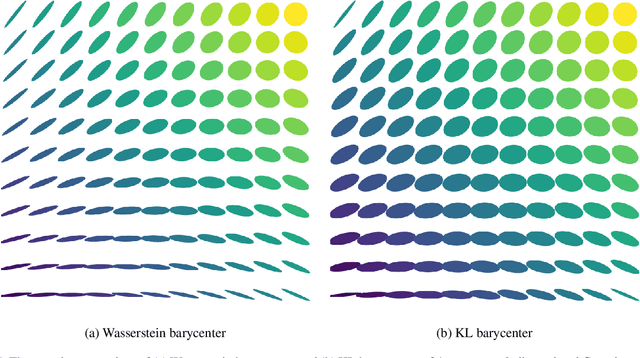
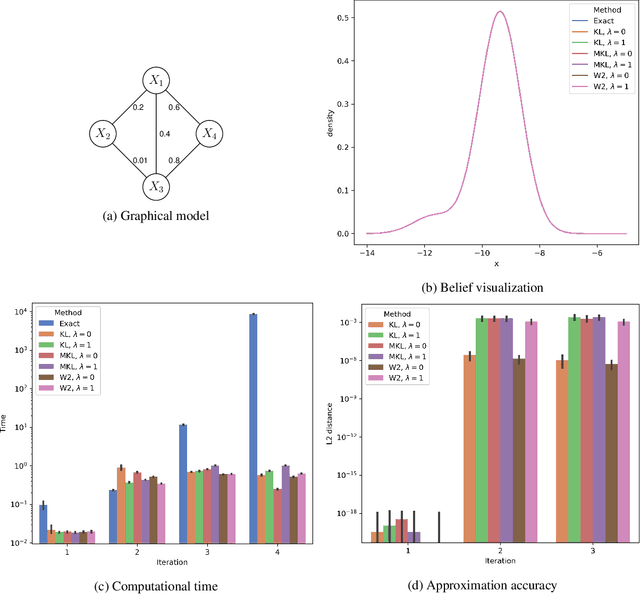
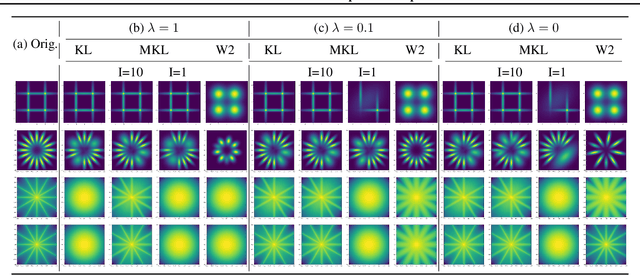
Gaussian mixture reduction (GMR) is the problem of approximating a finite Gaussian mixture by one with fewer components. It is widely used in density estimation, nonparametric belief propagation, and Bayesian recursive filtering. Although optimization and clustering-based algorithms have been proposed for GMR, they are either computationally expensive or lacking in theoretical supports. In this work, we propose to perform GMR by minimizing the entropic regularized composite transportation distance between two mixtures. We show our approach provides a unified framework for GMR that is both interpretable and computationally efficient. Our work also bridges the gap between optimization and clustering-based approaches for GMR. A Majorization-Minimization algorithm is developed for our optimization problem and its theoretical convergence is also established in this paper. Empirical experiments are also conducted to show the effectiveness of GMR. The effect of the choice of transportation cost on the performance of GMR is also investigated.