Q-learning for Quantile MDPs: A Decomposition, Performance, and Convergence Analysis

In Markov decision processes (MDPs), quantile risk measures such as Value-at-Risk are a standard metric for modeling RL agents' preferences for certain outcomes. This paper proposes a new Q-learning algorithm for quantile optimization in MDPs with strong convergence and performance guarantees. The algorithm leverages a new, simple dynamic program (DP) decomposition for quantile MDPs. Compared with prior work, our DP decomposition requires neither known transition probabilities nor solving complex saddle point equations and serves as a suitable foundation for other model-free RL algorithms. Our numerical results in tabular domains show that our Q-learning algorithm converges to its DP variant and outperforms earlier algorithms.

On Dynamic Program Decompositions of Static Risk Measures

Optimizing static risk-averse objectives in Markov decision processes is challenging because they do not readily admit dynamic programming decompositions. Prior work has proposed to use a dynamic decomposition of risk measures that help to formulate dynamic programs on an augmented state space. This paper shows that several existing decompositions are inherently inexact, contradicting several claims in the literature. In particular, we give examples that show that popular decompositions for CVaR and EVaR risk measures are strict overestimates of the true risk values. However, an exact decomposition is possible for VaR, and we give a simple proof that illustrates the fundamental difference between VaR and CVaR dynamic programming properties.

RASR: Risk-Averse Soft-Robust MDPs with EVaR and Entropic Risk

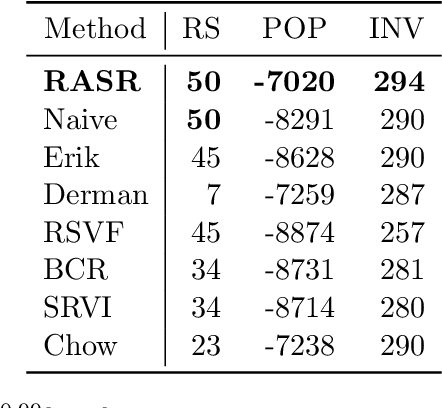
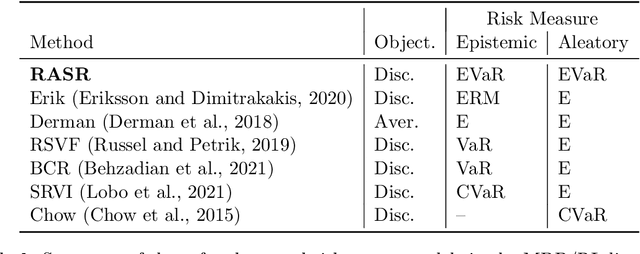
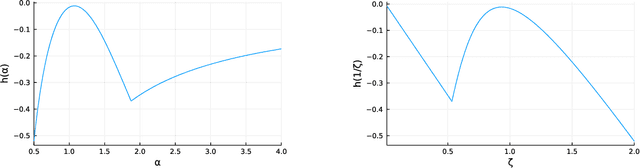
Prior work on safe Reinforcement Learning (RL) has studied risk-aversion to randomness in dynamics (aleatory) and to model uncertainty (epistemic) in isolation. We propose and analyze a new framework to jointly model the risk associated with epistemic and aleatory uncertainties in finite-horizon and discounted infinite-horizon MDPs. We call this framework that combines Risk-Averse and Soft-Robust methods RASR. We show that when the risk-aversion is defined using either EVaR or the entropic risk, the optimal policy in RASR can be computed efficiently using a new dynamic program formulation with a time-dependent risk level. As a result, the optimal risk-averse policies are deterministic but time-dependent, even in the infinite-horizon discounted setting. We also show that particular RASR objectives reduce to risk-averse RL with mean posterior transition probabilities. Our empirical results show that our new algorithms consistently mitigate uncertainty as measured by EVaR and other standard risk measures.