Intermediate Results on the Complexity of STRIPS$_{1}^{1}$

This paper is based on Bylander's results on the computational complexity of propositional STRIPS planning. He showed that when only ground literals are permitted, determining plan existence is PSPACE-complete even if operators are limited to two preconditions and two postconditions. While NP-hardness is settled, it is unknown whether propositional STRIPS with operators that only have one precondition and one effect is NP-complete. We shed light on the question whether this small solution hypothesis for STRIPS$^1_1$ is true, calling a SAT solver for small instances, introducing the literal graph, and mapping it to Petri nets.

A New Arc-Routing Algorithm Applied to Winter Road Maintenance

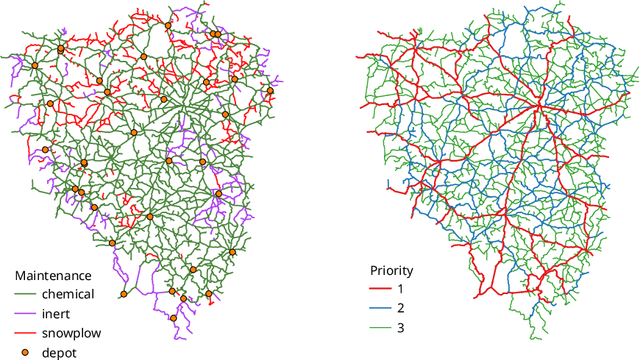
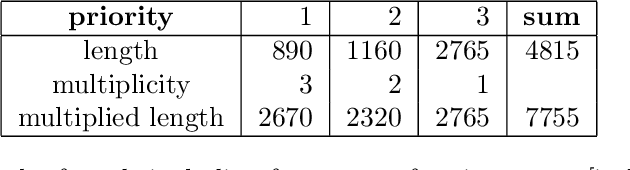
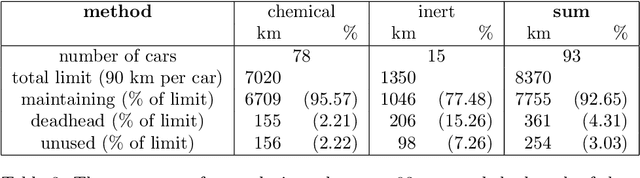
This paper studies large scale instances of a fairly general arc-routing problem as well as incorporate practical constraints in particular coming from the scheduling problem of the winter road maintenance (e.g. different priorities for and methods of road maintenance). We develop a new algorithm based on a bin-packing heuristic which is well-scalable and able to solve road networks on thousands of crossroads and road segments in few minutes. Since it is impossible to find an optimal solution for such a large instances to compare it with a result of our algorithm, we also develop techniques to compute lower bounds which are based on Integer Linear Programming and Lazy Constraints.