Probably certifiably correct k-means clustering

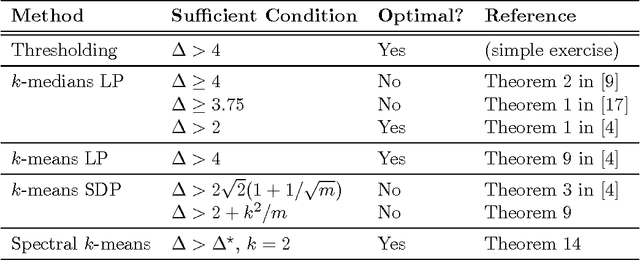
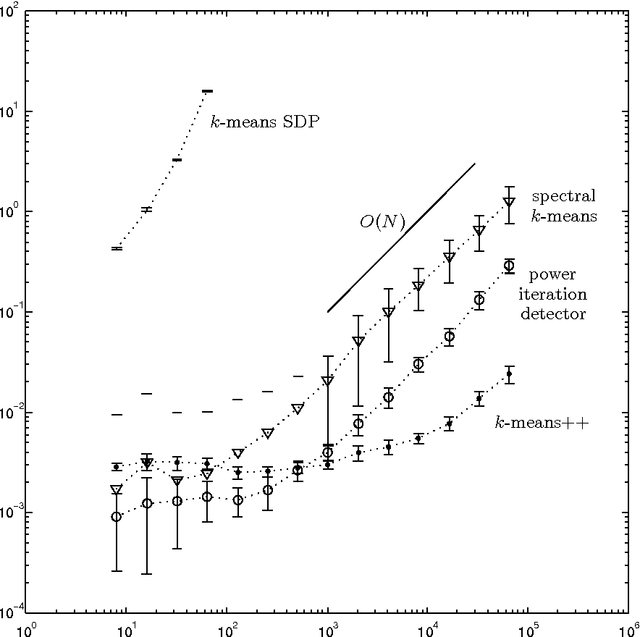
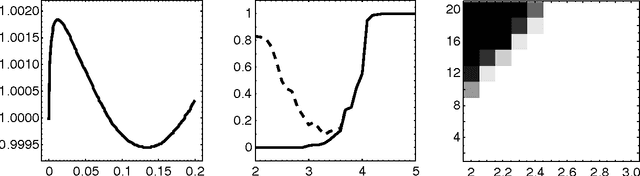
Recently, Bandeira [arXiv:1509.00824] introduced a new type of algorithm (the so-called probably certifiably correct algorithm) that combines fast solvers with the optimality certificates provided by convex relaxations. In this paper, we devise such an algorithm for the problem of k-means clustering. First, we prove that Peng and Wei's semidefinite relaxation of k-means is tight with high probability under a distribution of planted clusters called the stochastic ball model. Our proof follows from a new dual certificate for integral solutions of this semidefinite program. Next, we show how to test the optimality of a proposed k-means solution using this dual certificate in quasilinear time. Finally, we analyze a version of spectral clustering from Peng and Wei that is designed to solve k-means in the case of two clusters. In particular, we show that this quasilinear-time method typically recovers planted clusters under the stochastic ball model.

Learning Boolean functions with concentrated spectra

This paper discusses the theory and application of learning Boolean functions that are concentrated in the Fourier domain. We first estimate the VC dimension of this function class in order to establish a small sample complexity of learning in this case. Next, we propose a computationally efficient method of empirical risk minimization, and we apply this method to the MNIST database of handwritten digits. These results demonstrate the effectiveness of our model for modern classification tasks. We conclude with a list of open problems for future investigation.

On the tightness of an SDP relaxation of k-means

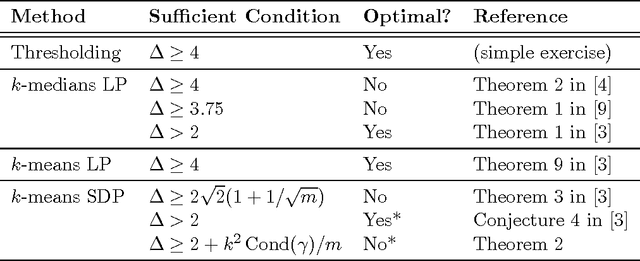
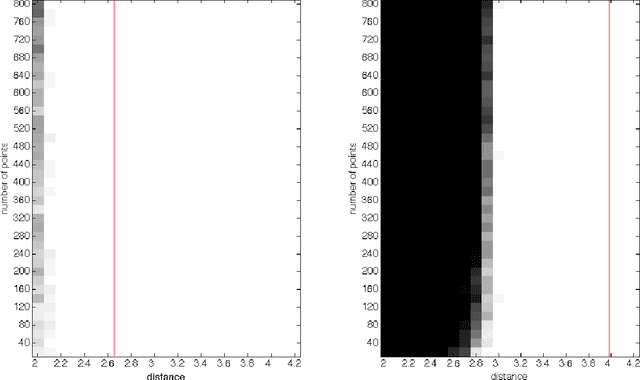
Recently, Awasthi et al. introduced an SDP relaxation of the $k$-means problem in $\mathbb R^m$. In this work, we consider a random model for the data points in which $k$ balls of unit radius are deterministically distributed throughout $\mathbb R^m$, and then in each ball, $n$ points are drawn according to a common rotationally invariant probability distribution. For any fixed ball configuration and probability distribution, we prove that the SDP relaxation of the $k$-means problem exactly recovers these planted clusters with probability $1-e^{-\Omega(n)}$ provided the distance between any two of the ball centers is $>2+\epsilon$, where $\epsilon$ is an explicit function of the configuration of the ball centers, and can be arbitrarily small when $m$ is large.