On the tightness of an SDP relaxation of k-means
Paper and Code
May 18, 2015
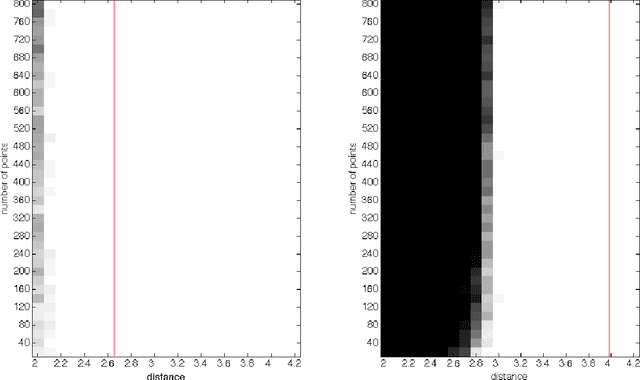
Recently, Awasthi et al. introduced an SDP relaxation of the $k$-means problem in $\mathbb R^m$. In this work, we consider a random model for the data points in which $k$ balls of unit radius are deterministically distributed throughout $\mathbb R^m$, and then in each ball, $n$ points are drawn according to a common rotationally invariant probability distribution. For any fixed ball configuration and probability distribution, we prove that the SDP relaxation of the $k$-means problem exactly recovers these planted clusters with probability $1-e^{-\Omega(n)}$ provided the distance between any two of the ball centers is $>2+\epsilon$, where $\epsilon$ is an explicit function of the configuration of the ball centers, and can be arbitrarily small when $m$ is large.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge