Function Trees: Transparent Machine Learning

The output of a machine learning algorithm can usually be represented by one or more multivariate functions of its input variables. Knowing the global properties of such functions can help in understanding the system that produced the data as well as interpreting and explaining corresponding model predictions. A method is presented for representing a general multivariate function as a tree of simpler functions. This tree exposes the global internal structure of the function by uncovering and describing the combined joint influences of subsets of its input variables. Given the inputs and corresponding function values, a function tree is constructed that can be used to rapidly identify and compute all of the function's main and interaction effects up to high order. Interaction effects involving up to four variables are graphically visualized.

Lockout: Sparse Regularization of Neural Networks

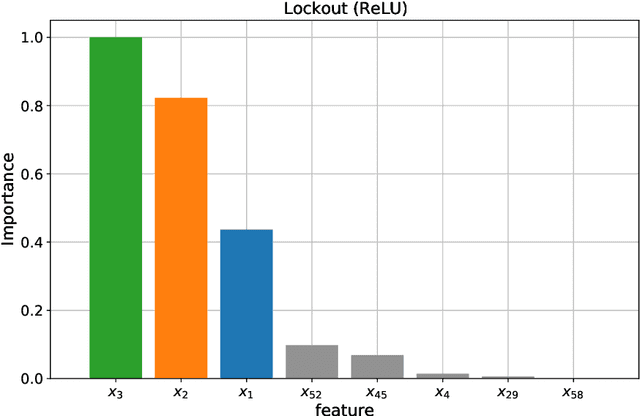
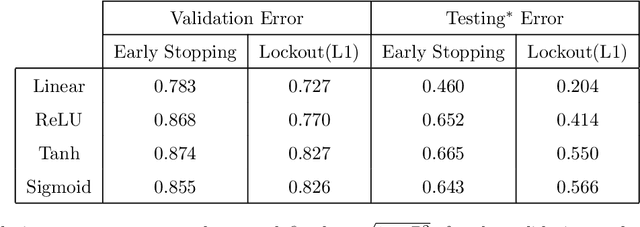
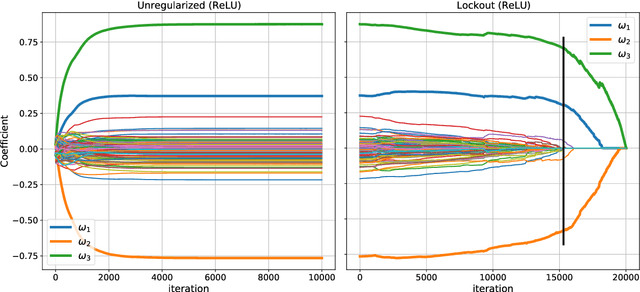
Many regression and classification procedures fit a parameterized function $f(x;w)$ of predictor variables $x$ to data $\{x_{i},y_{i}\}_1^N$ based on some loss criterion $L(y,f)$. Often, regularization is applied to improve accuracy by placing a constraint $P(w)\leq t$ on the values of the parameters $w$. Although efficient methods exist for finding solutions to these constrained optimization problems for all values of $t\geq0$ in the special case when $f$ is a linear function, none are available when $f$ is non-linear (e.g. Neural Networks). Here we present a fast algorithm that provides all such solutions for any differentiable function $f$ and loss $L$, and any constraint $P$ that is an increasing monotone function of the absolute value of each parameter. Applications involving sparsity inducing regularization of arbitrary Neural Networks are discussed. Empirical results indicate that these sparse solutions are usually superior to their dense counterparts in both accuracy and interpretability. This improvement in accuracy can often make Neural Networks competitive with, and sometimes superior to, state-of-the-art methods in the analysis of tabular data.

Predicting Regression Probability Distributions with Imperfect Data Through Optimal Transformations

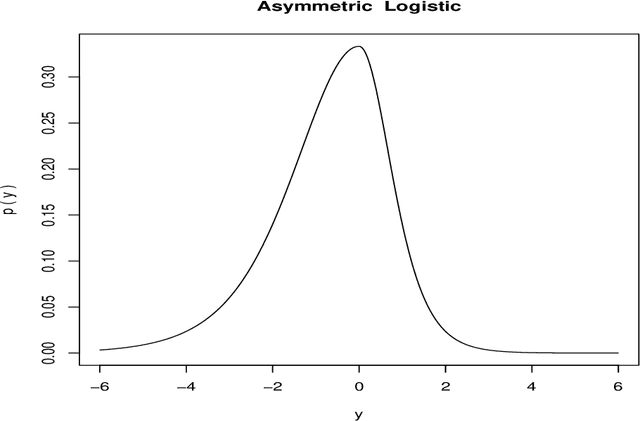
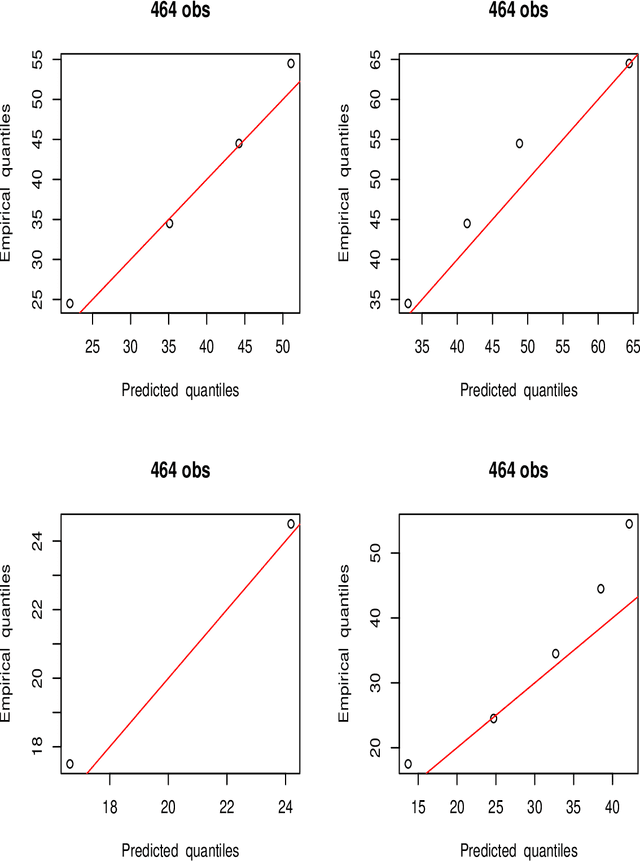
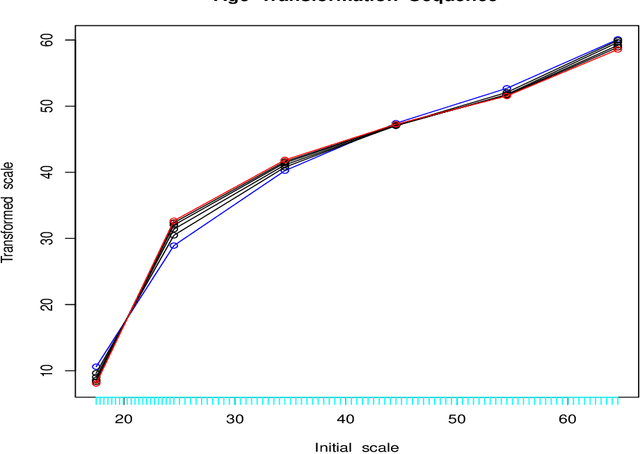
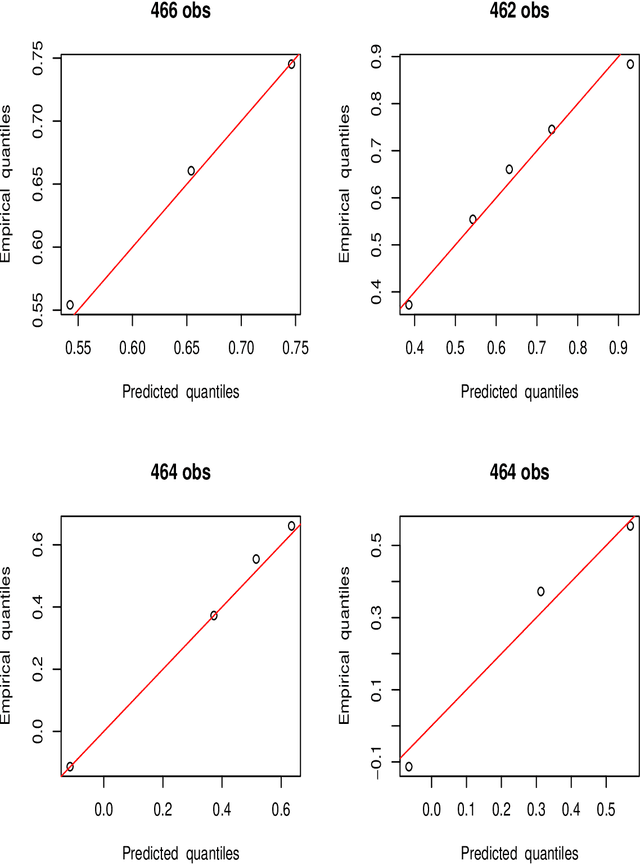
The goal of regression analysis is to predict the value of a numeric outcome variable y given a vector of joint values of other (predictor) variables x. Usually a particular x-vector does not specify a repeatable value for y, but rather a probability distribution of possible y--values, p(y|x). This distribution has a location, scale and shape, all of which can depend on x, and are needed to infer likely values for y given x. Regression methods usually assume that training data y-values are perfect numeric realizations from some well behaived p(y|x). Often actual training data y-values are discrete, truncated and/or arbitrary censored. Regression procedures based on an optimal transformation strategy are presented for estimating location, scale and shape of p(y|x) as general functions of x, in the possible presence of such imperfect training data. In addition, validation diagnostics are presented to ascertain the quality of the solutions.

Contrast Trees and Distribution Boosting

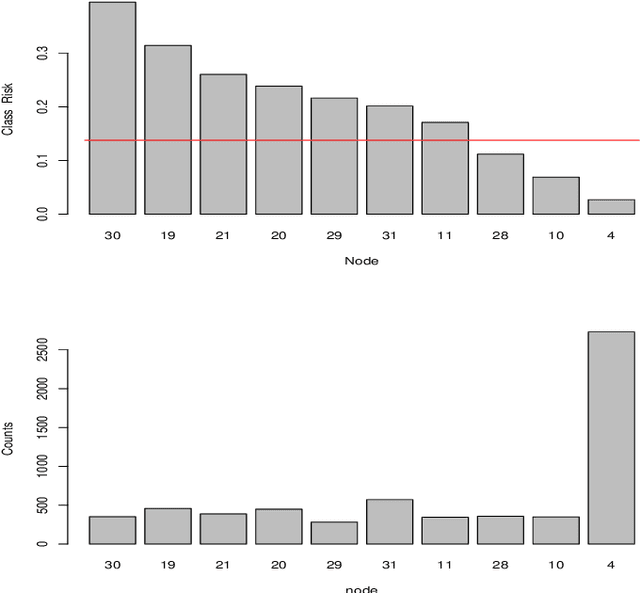
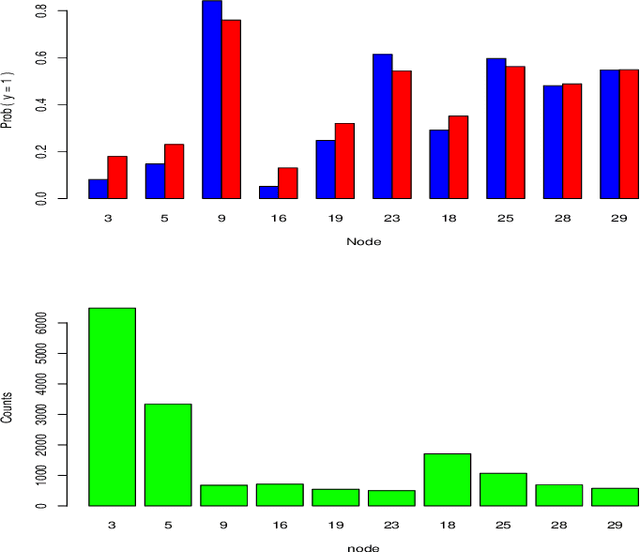
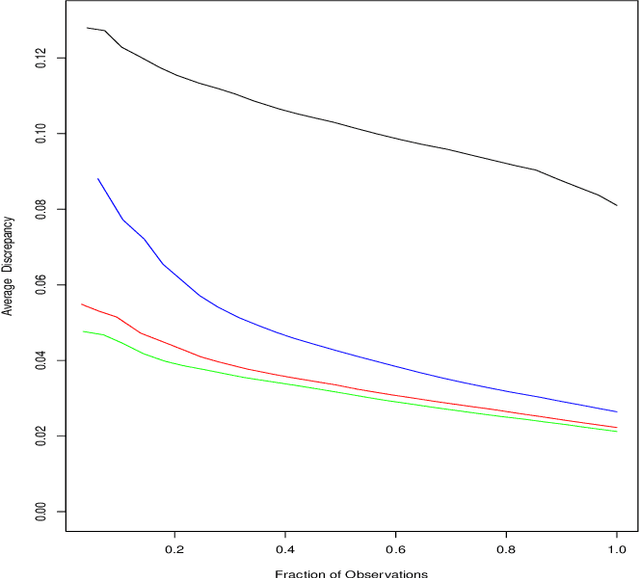
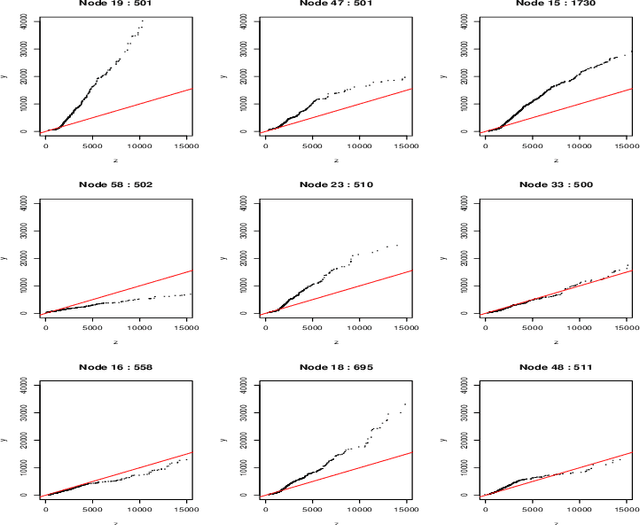
Often machine learning methods are applied and results reported in cases where there is little to no information concerning accuracy of the output. Simply because a computer program returns a result does not insure its validity. If decisions are to be made based on such results it is important to have some notion of their veracity. Contrast trees represent a new approach for assessing the accuracy of many types of machine learning estimates that are not amenable to standard (cross) validation methods. In situations where inaccuracies are detected boosted contrast trees can often improve performance. A special case, distribution boosting, provides an assumption free method for estimating the full probability distribution of an outcome variable given any set of joint input predictor variable values.