Wilmer Arbelo
Lockout: Sparse Regularization of Neural Networks
Jul 15, 2021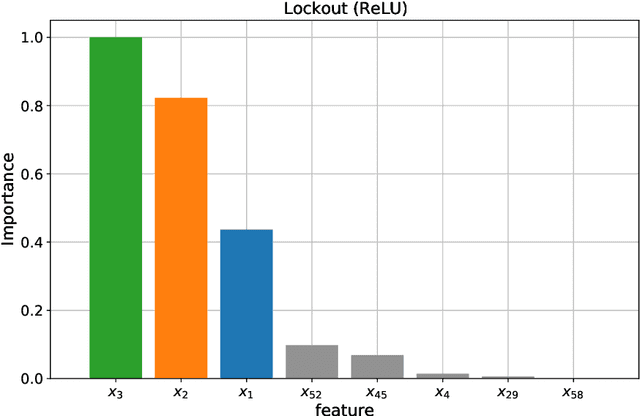
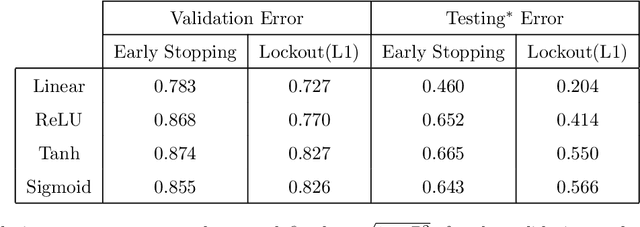
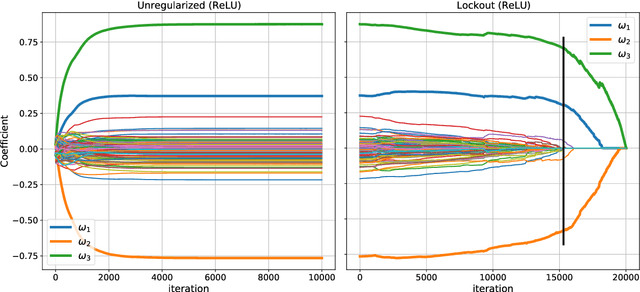

Abstract:Many regression and classification procedures fit a parameterized function $f(x;w)$ of predictor variables $x$ to data $\{x_{i},y_{i}\}_1^N$ based on some loss criterion $L(y,f)$. Often, regularization is applied to improve accuracy by placing a constraint $P(w)\leq t$ on the values of the parameters $w$. Although efficient methods exist for finding solutions to these constrained optimization problems for all values of $t\geq0$ in the special case when $f$ is a linear function, none are available when $f$ is non-linear (e.g. Neural Networks). Here we present a fast algorithm that provides all such solutions for any differentiable function $f$ and loss $L$, and any constraint $P$ that is an increasing monotone function of the absolute value of each parameter. Applications involving sparsity inducing regularization of arbitrary Neural Networks are discussed. Empirical results indicate that these sparse solutions are usually superior to their dense counterparts in both accuracy and interpretability. This improvement in accuracy can often make Neural Networks competitive with, and sometimes superior to, state-of-the-art methods in the analysis of tabular data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge