Predicting Regression Probability Distributions with Imperfect Data Through Optimal Transformations
Paper and Code
Jan 27, 2020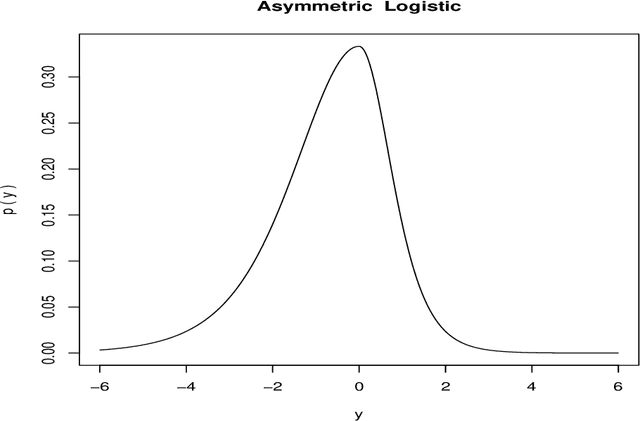
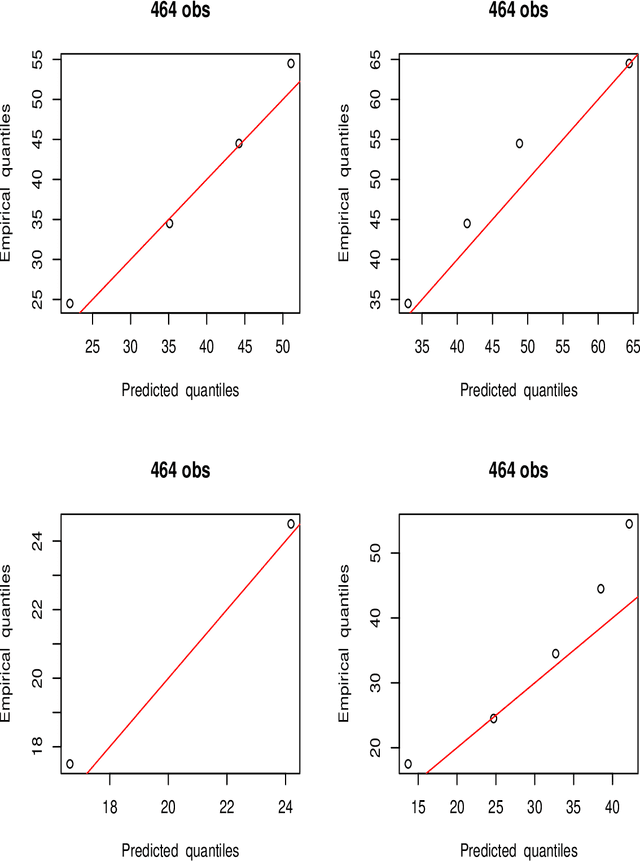
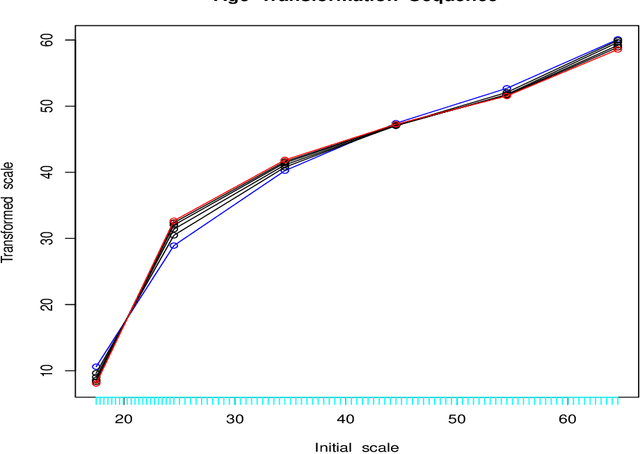
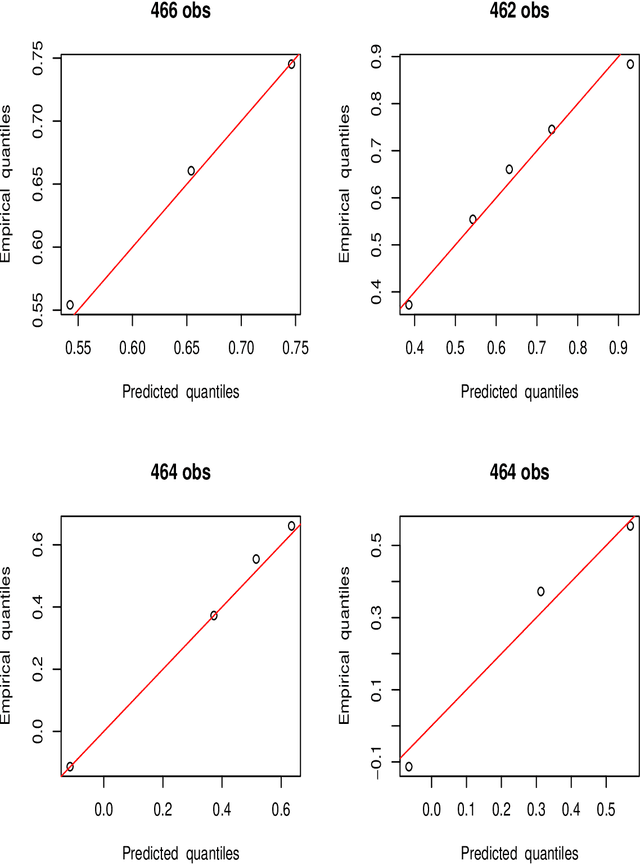
The goal of regression analysis is to predict the value of a numeric outcome variable y given a vector of joint values of other (predictor) variables x. Usually a particular x-vector does not specify a repeatable value for y, but rather a probability distribution of possible y--values, p(y|x). This distribution has a location, scale and shape, all of which can depend on x, and are needed to infer likely values for y given x. Regression methods usually assume that training data y-values are perfect numeric realizations from some well behaived p(y|x). Often actual training data y-values are discrete, truncated and/or arbitrary censored. Regression procedures based on an optimal transformation strategy are presented for estimating location, scale and shape of p(y|x) as general functions of x, in the possible presence of such imperfect training data. In addition, validation diagnostics are presented to ascertain the quality of the solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge