USEFUSE: Utile Stride for Enhanced Performance in Fused Layer Architecture of Deep Neural Networks

Convolutional Neural Networks (CNNs) are crucial in various applications, but their deployment on resource-constrained edge devices poses challenges. This study presents the Sum-of-Products (SOP) units for convolution, which utilize low-latency left-to-right bit-serial arithmetic to minimize response time and enhance overall performance. The study proposes a methodology for fusing multiple convolution layers to reduce off-chip memory communication and increase overall performance. An effective mechanism detects and skips inefficient convolutions after ReLU layers, minimizing power consumption without compromising accuracy. Furthermore, efficient tile movement guarantees uniform access to the fusion pyramid. An analysis demonstrates the utile stride strategy improves operational intensity. Two designs cater to varied demands: one focuses on minimal response time for mission-critical applications, and another focuses on resource-constrained devices with comparable latency. This approach notably reduced redundant computations, improving the efficiency of CNN deployment on edge devices.

Forward and Reverse Converters for the Moduli-Set $\{2^{2q+1},2^q+2^{q-1}\pm1\}$

Modulo-$(2^q + 2^{q-1} \pm 1)$ adders have recently been implemented using the regular parallel prefix (RPP) architecture, matching the speed of the widely used modulo-$(2^q \pm 1)$ RPP adders. Consequently, we introduce a new moduli set $\tau^+ = \{2^{2q+1}, 2^q + 2^{q-1} \pm 1\}$, with over $(2^{q+2}) \times$ dynamic range and adder speeds comparable to the conventional $\tau = \{2^q, 2^q \pm 1\}$ set. However, to fully leverage $\tau^+$ in residue number system applications, a complete set of circuitries is necessary. This work focuses on the design and implementation of the forward and reverse converters for $\tau^+$. These converters consist of four and seven levels of carry-save addition units, culminating in a final modulo-$(2^q + 2^{q-1} \pm 1)$ and modulo-$(2^{2q+1} + 2^{2q-2} - 1)$ adder, respectively. Through analytical evaluations and circuit simulations, we demonstrate that the overall performance of a sequence of operations including residue generation -- including residue generation, $k$ additions, and reverse conversion -- using $\tau^+$ surpasses that of $\tau$ when $k$ exceeds a certain practical threshold.

Enhancing Computational Efficiency in Intensive Domains via Redundant Residue Number Systems

In computation-intensive domains such as digital signal processing, encryption, and neural networks, the performance of arithmetic units, including adders and multipliers, is pivotal. Conventional numerical systems often fall short of meeting the efficiency requirements of these applications concerning area, time, and power consumption. Innovative approaches like residue number systems (RNS) and redundant number systems have been introduced to surmount this challenge, markedly elevating computational efficiency. This paper examines from multiple perspectives how the fusion of redundant number systems with RNS (termed R-RNS) can diminish latency and enhance circuit implementation, yielding substantial benefits in practical scenarios. We conduct a comparative analysis of four systems - RNS, redundant number system, Binary Number System (BNS), and Signed-Digit Redundant Residue Number System (SD-RNS)-and appraise SD-RNS through an advanced Deep Neural Network (DNN) utilizing the CIFAR-10 dataset. Our findings are encouraging, demonstrating that SD-RNS attains computational speedups of 1.27 times and 2.25 times over RNS and BNS, respectively, and reduces energy consumption by 60% compared to BNS during sequential addition and multiplication tasks.

DSLOT-NN: Digit-Serial Left-to-Right Neural Network Accelerator

We propose a Digit-Serial Left-tO-righT (DSLOT) arithmetic based processing technique called DSLOT-NN with aim to accelerate inference of the convolution operation in the deep neural networks (DNNs). The proposed work has the ability to assess and terminate the ineffective convolutions which results in massive power and energy savings. The processing engine is comprised of low-latency most-significant-digit-first (MSDF) (also called online) multipliers and adders that processes data from left-to-right, allowing the execution of subsequent operations in digit-pipelined manner. Use of online operators eliminates the need for the development of complex mechanism of identifying the negative activation, as the output with highest weight value is generated first, and the sign of the result can be identified as soon as first non-zero digit is generated. The precision of the online operators can be tuned at run-time, making them extremely useful in situations where accuracy can be compromised for power and energy savings. The proposed design has been implemented on Xilinx Virtex-7 FPGA and is compared with state-of-the-art Stripes on various performance metrics. The results show the proposed design presents power savings, has shorter cycle time, and approximately 50% higher OPS per watt.

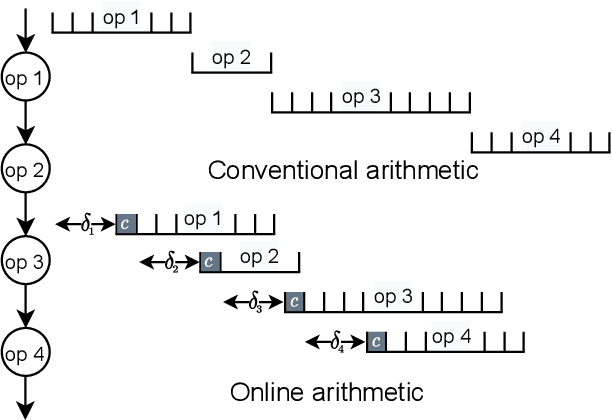
Low-Latency Online Multiplier with Reduced Activities and Minimized Interconnect for Inner Product Arrays

Multiplication is indispensable and is one of the core operations in many modern applications including signal processing and neural networks. Conventional right-to-left (RL) multiplier extensively contributes to the power consumption, area utilization and critical path delay in such applications. This paper proposes a low latency multiplier based on online or left-to-right (LR) arithmetic which can increase throughput and reduce latency by digit-level pipelining. Online arithmetic enables overlapping successive operations regardless of data dependency because of the most significant digit first mode of operation. To produce most significant digit first, it uses redundant number system and we can have a carry-free addition, therefore, the delay of the arithmetic operation is independent of operand bit width. The operations are performed digit by digit serially from left to right which allows gradual increase in the slice activities making it suitable for implementation on reconfigurable devices. Serial nature of the online algorithm and gradual increment/decrement of active slices minimize the interconnects and signal activities resulting in overall reduction of area and power consumption. We present online multipliers with; both inputs in serial, and one in serial and one in parallel. Pipelined and non-pipelined designs of the proposed multipliers have been synthesized with GSCL 45nm technology on Synopsys Design Compiler. Thorough comparative analysis has been performed using widely used performance metrics. The results show that the proposed online multipliers outperform the RL multipliers.

Multiplier with Reduced Activities and Minimized Interconnect for Inner Product Arrays

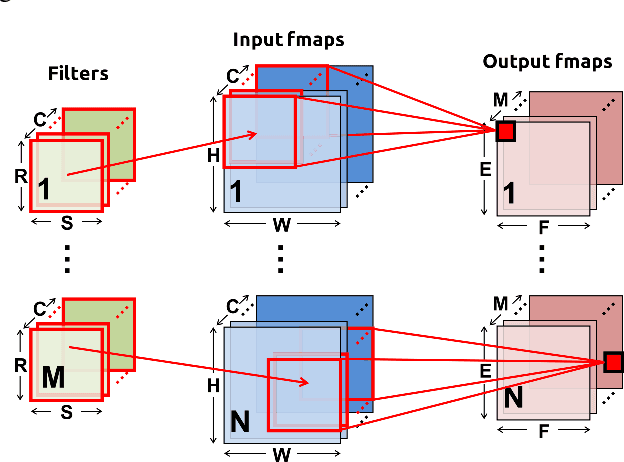
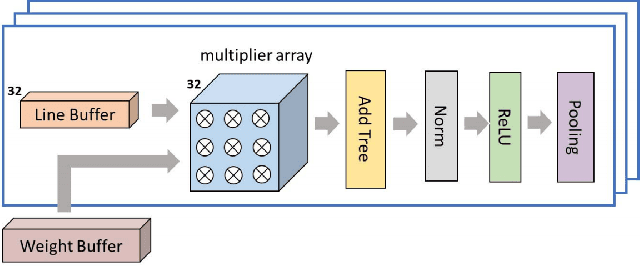
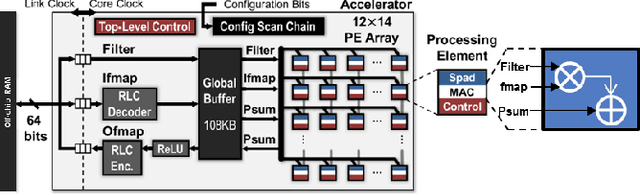
We present a pipelined multiplier with reduced activities and minimized interconnect based on online digit-serial arithmetic. The working precision has been truncated such that $p<n$ bits are used to compute $n$ bits product, resulting in significant savings in area and power. The digit slices follow variable precision according to input, increasing upto $p$ and then decreases according to the error profile. Pipelining has been done to achieve high throughput and low latency which is desirable for compute intensive inner products. Synthesis results of the proposed designs have been presented and compared with the non-pipelined online multiplier, pipelined online multiplier with full working precision and conventional serial-parallel and array multipliers. For $8, 16, 24$ and $32$ bit precision, the proposed low power pipelined design show upto $38\%$ and $44\%$ reduction in power and area respectively compared to the pipelined online multiplier without working precision truncation.