Flexible mean field variational inference using mixtures of non-overlapping exponential families

Sparse models are desirable for many applications across diverse domains as they can perform automatic variable selection, aid interpretability, and provide regularization. When fitting sparse models in a Bayesian framework, however, analytically obtaining a posterior distribution over the parameters of interest is intractable for all but the simplest cases. As a result practitioners must rely on either sampling algorithms such as Markov chain Monte Carlo or variational methods to obtain an approximate posterior. Mean field variational inference is a particularly simple and popular framework that is often amenable to analytically deriving closed-form parameter updates. When all distributions in the model are members of exponential families and are conditionally conjugate, optimization schemes can often be derived by hand. Yet, I show that using standard mean field variational inference can fail to produce sensible results for models with sparsity-inducing priors, such as the spike-and-slab. Fortunately, such pathological behavior can be remedied as I show that mixtures of exponential family distributions with non-overlapping support form an exponential family. In particular, any mixture of a diffuse exponential family and a point mass at zero to model sparsity forms an exponential family. Furthermore, specific choices of these distributions maintain conditional conjugacy. I use two applications to motivate these results: one from statistical genetics that has connections to generalized least squares with a spike-and-slab prior on the regression coefficients; and sparse probabilistic principal component analysis. The theoretical results presented here are broadly applicable beyond these two examples.

A Likelihood-Free Inference Framework for Population Genetic Data using Exchangeable Neural Networks

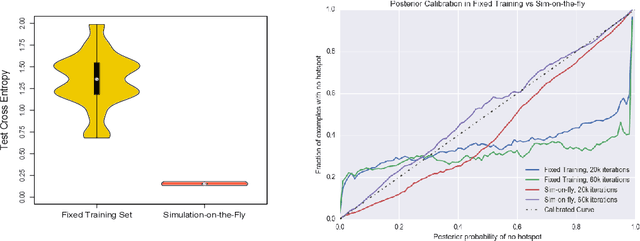
An explosion of high-throughput DNA sequencing in the past decade has led to a surge of interest in population-scale inference with whole-genome data. Recent work in population genetics has centered on designing inference methods for relatively simple model classes, and few scalable general-purpose inference techniques exist for more realistic, complex models. To achieve this, two inferential challenges need to be addressed: (1) population data are exchangeable, calling for methods that efficiently exploit the symmetries of the data, and (2) computing likelihoods is intractable as it requires integrating over a set of correlated, extremely high-dimensional latent variables. These challenges are traditionally tackled by likelihood-free methods that use scientific simulators to generate datasets and reduce them to hand-designed, permutation-invariant summary statistics, often leading to inaccurate inference. In this work, we develop an exchangeable neural network that performs summary statistic-free, likelihood-free inference. Our framework can be applied in a black-box fashion across a variety of simulation-based tasks, both within and outside biology. We demonstrate the power of our approach on the recombination hotspot testing problem, outperforming the state-of-the-art.