ReloPush: Multi-object Rearrangement in Confined Spaces with a Nonholonomic Mobile Robot Pusher

We focus on the problem of rearranging a set of objects within a confined space with a nonholonomically constrained mobile robot pusher. This problem is relevant to many real-world domains, including warehouse automation and construction. These domains give rise to instances involving a combination of geometric, kinematic, and physics constraints, which make planning particularly challenging. Prior work often makes simplifying assumptions like the use of holonomic mobile robots or dexterous manipulators capable of unconstrained overhand reaching. Our key insight is we can empower even a constrained mobile pusher to tackle complex rearrangement tasks by enabling it to modify the environment to its favor in a constraint-aware fashion. To this end, we describe a Push-Traversability graph, whose vertices represent poses that the pusher can push objects from and edges represent optimal, kinematically feasible, and stable push-rearrangements of objects. Based on this graph, we develop ReloPush, a planning framework that leverages Dubins curves and standard graph search techniques to generate an efficient sequence of object rearrangements to be executed by the pusher. We evaluate ReloPush across a series of challenging scenarios, involving the rearrangement of densely cluttered workspaces with up to eight objects by a 1tenth mobile robot pusher. ReloPush exhibits orders of magnitude faster runtimes and significantly more robust execution in the real world, evidenced in lower execution times and fewer losses of object contact, compared to two baselines lacking our proposed graph structure.

Ordered sorting of cluttered objects using multiple mobile manipulators

We present a search-based planning algorithm to sort objects in clutter using a multi-robot team. We consider the object rearrangement problem in which the objects must be sorted into different groups in a particular order. In clutter, the order constraints could not be easily satisfied since some objects occlude other objects. Those objects occluding others need to be moved more than once to make the occluded objects accessible. This nonmonotone class of the rearrangement prob- lem with order constraints becomes harder if multiple robots are involved, which practically mandates proper computations of robot allocations. The proposed method first finds a sequence of objects to be sorted using a search such that the order constraint in each group is satisfied. The search can solve nonmonotone instances that require temporal relocation of some objects to access the next object to be sorted. Once a complete sorting sequence is found, the objects in the sequence are assigned to multiple mobile manipulators using a greedy allocation method. We develop four versions of the method with different search strategies. In the experiments, we show that our method can find a sorting sequence quickly (e.g., 4.6 sec with 20 objects sorted into five groups) even though the solved instances include hard nonmonotone ones. The extensive tests and the experiments in simulation show the ability of the method to solve the real-world sorting problem using multiple mobile manipulators.

Coordination of two robotic manipulators for object retrieval in clutter

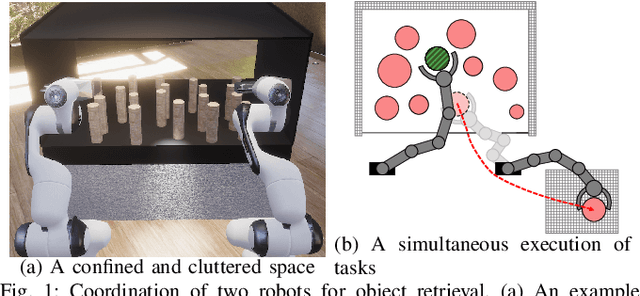
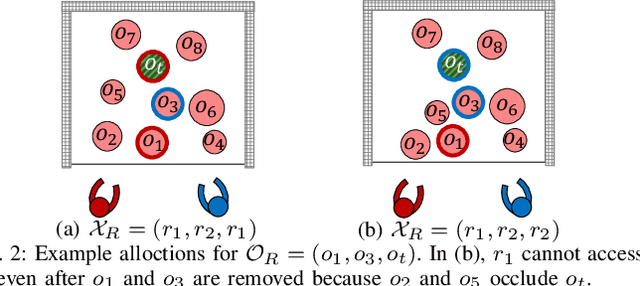
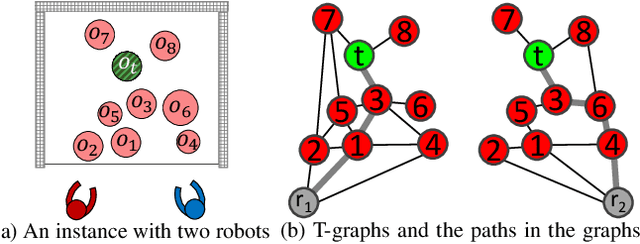
We consider the problem of retrieving a target object from a confined space by two robotic manipulators where overhand grasps are not allowed. If other movable obstacles occlude the target, more than one object should be relocated to clear the path to reach the target object. With two robots, the relocation could be done efficiently by simultaneously performing relocation tasks. However, the precedence constraint between the tasks (e.g, some objects at the front should be removed to manipulate the objects in the back) makes the simultaneous task execution difficult. We propose a coordination method that determines which robot relocates which object so as to perform tasks simultaneously. Given a set of objects to be relocated, the objective is to maximize the number of turn-takings of the robots in performing relocation tasks. Thus, one robot can pick an object in the clutter while the other robot places an object in hand to the outside of the clutter. However, the object to be relocated may not be accessible to all robots, so taking turns could not always be achieved. Our method is based on the optimal uniform-cost search so the number of turn-takings is proven to be maximized. We also propose a greedy variant whose computation time is shorter. From experiments, we show that our method reduces the completion time of the mission by at least 22.9% (at most 27.3%) compared to the methods with no consideration of turn-taking.