Analyzing Neural Network Information Flow Using Differential Geometry

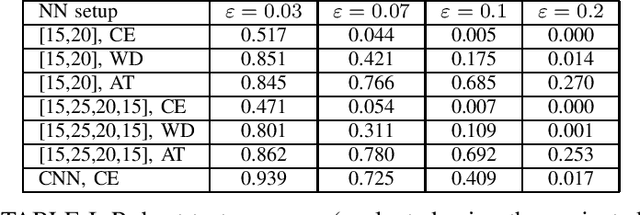
This paper provides a fresh view of the neural network (NN) data flow problem, i.e., identifying the NN connections that are most important for the performance of the full model, through the lens of graph theory. Understanding the NN data flow provides a tool for symbolic NN analysis, e.g.,~robustness analysis or model repair. Unlike the standard approach to NN data flow analysis, which is based on information theory, we employ the notion of graph curvature, specifically Ollivier-Ricci curvature (ORC). The ORC has been successfully used to identify important graph edges in various domains such as road traffic analysis, biological and social networks. In particular, edges with negative ORC are considered bottlenecks and as such are critical to the graph's overall connectivity, whereas positive-ORC edges are not essential. We use this intuition for the case of NNs as well: we 1)~construct a graph induced by the NN structure and introduce the notion of neural curvature (NC) based on the ORC; 2)~calculate curvatures based on activation patterns for a set of input examples; 3)~aim to demonstrate that NC can indeed be used to rank edges according to their importance for the overall NN functionality. We evaluate our method through pruning experiments and show that removing negative-ORC edges quickly degrades the overall NN performance, whereas positive-ORC edges have little impact. The proposed method is evaluated on a variety of models trained on three image datasets, namely MNIST, CIFAR-10 and CIFAR-100. The results indicate that our method can identify a larger number of unimportant edges as compared to state-of-the-art pruning methods.

Analyzing Neural Network Robustness Using Graph Curvature

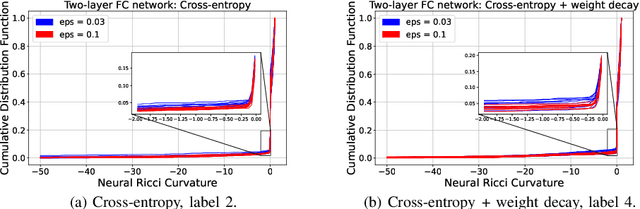
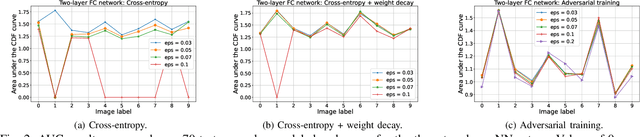
This paper presents a new look at the neural network (NN) robustness problem, from the point of view of graph theory analysis, specifically graph curvature. Graph curvature (e.g., Ricci curvature) has been used to analyze system dynamics and identify bottlenecks in many domains, including road traffic analysis and internet routing. We define the notion of neural Ricci curvature and use it to identify bottleneck NN edges that are heavily used to ``transport data" to the NN outputs. We provide an evaluation on MNIST that illustrates that such edges indeed occur more frequently for inputs where NNs are less robust. These results will serve as the basis for an alternative method of robust training, by minimizing the number of bottleneck edges.