Shallow-circuit Supervised Learning on a Quantum Processor

Quantum computing has long promised transformative advances in data analysis, yet practical quantum machine learning has remained elusive due to fundamental obstacles such as a steep quantum cost for the loading of classical data and poor trainability of many quantum machine learning algorithms designed for near-term quantum hardware. In this work, we show that one can overcome these obstacles by using a linear Hamiltonian-based machine learning method which provides a compact quantum representation of classical data via ground state problems for k-local Hamiltonians. We use the recent sample-based Krylov quantum diagonalization method to compute low-energy states of the data Hamiltonians, whose parameters are trained to express classical datasets through local gradients. We demonstrate the efficacy and scalability of the methods by performing experiments on benchmark datasets using up to 50 qubits of an IBM Heron quantum processor.

Phases of two-dimensional spinless lattice fermions with first-quantized deep neural-network quantum states

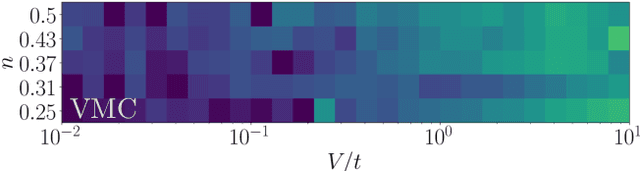
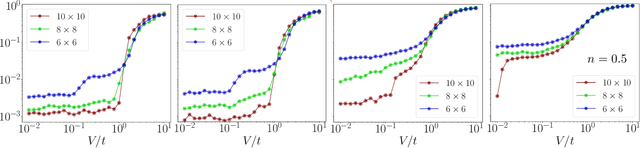
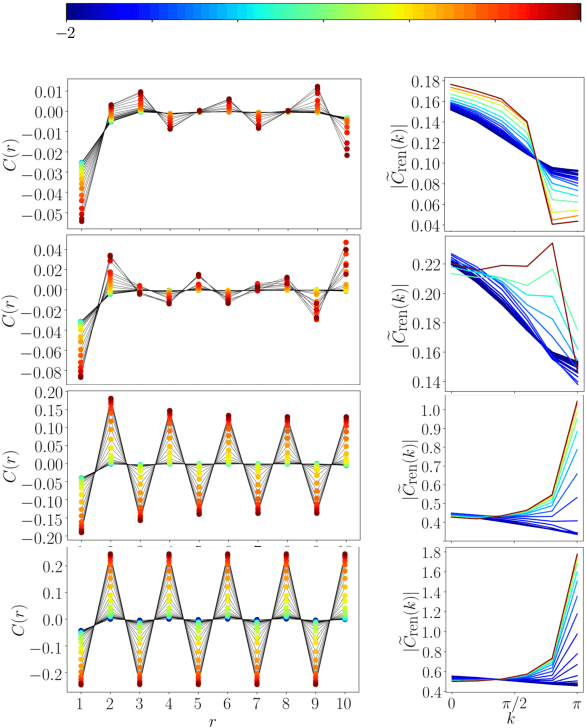
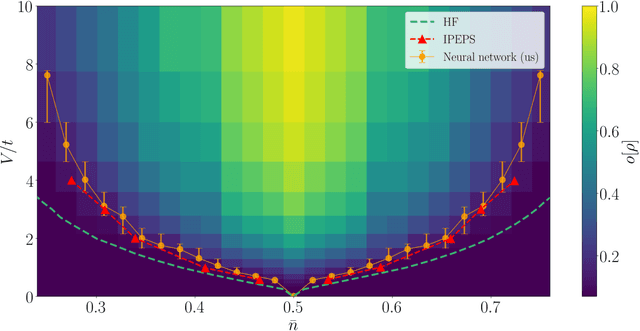
First-quantized deep neural network techniques are developed for analyzing strongly coupled fermionic systems on the lattice. Using a Slater-Jastrow inspired ansatz which exploits deep residual networks with convolutional residual blocks, we approximately determine the ground state of spinless fermions on a square lattice with nearest-neighbor interactions. The flexibility of the neural-network ansatz results in a high level of accuracy when compared to exact diagonalization results on small systems, both for energy and correlation functions. On large systems, we obtain accurate estimates of the boundaries between metallic and charge ordered phases as a function of the interaction strength and the particle density.