A Numerical Study of Chaotic Dynamics of K-S Equation with FNOs

Solving non-linear partial differential equations which exhibit chaotic dynamics is an important problem with a wide-range of applications such as predicting weather extremes and financial market risk. Fourier neural operators (FNOs) have been shown to be efficient in solving partial differential equations (PDEs). In this work we demonstrate simulation of dynamics in the chaotic regime of the two-dimensional (2d) Kuramoto-Sivashinsky equation using FNOs. Particularly, we analyze the effect of Fourier mode cutoff on the results obtained by using FNOs vs those obtained using traditional PDE solvers. We compare the outputs using metrics such as the 2d power spectrum and the radial power spectrum. In addition we propose the normalised error power spectrum which measures the percentage error in the FNO model outputs. We conclude that FNOs capture the dynamics in the chaotic regime of the 2d K-S equation, provided the Fourier mode cutoff is kept sufficiently high.

CLUDA : Contrastive Learning in Unsupervised Domain Adaptation for Semantic Segmentation

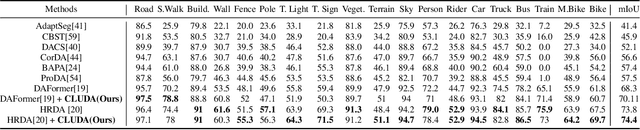
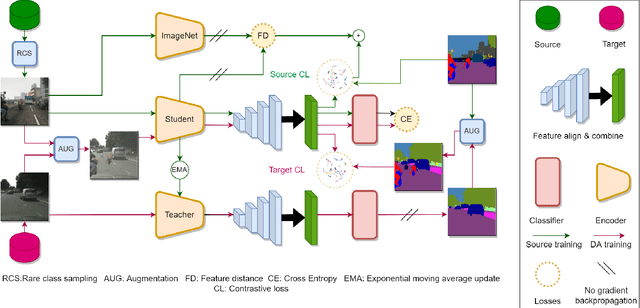
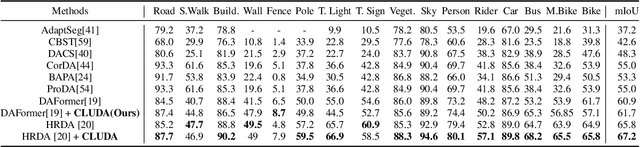
In this work, we propose CLUDA, a simple, yet novel method for performing unsupervised domain adaptation (UDA) for semantic segmentation by incorporating contrastive losses into a student-teacher learning paradigm, that makes use of pseudo-labels generated from the target domain by the teacher network. More specifically, we extract a multi-level fused-feature map from the encoder, and apply contrastive loss across different classes and different domains, via source-target mixing of images. We consistently improve performance on various feature encoder architectures and for different domain adaptation datasets in semantic segmentation. Furthermore, we introduce a learned-weighted contrastive loss to improve upon on a state-of-the-art multi-resolution training approach in UDA. We produce state-of-the-art results on GTA $\rightarrow$ Cityscapes (74.4 mIOU, +0.6) and Synthia $\rightarrow$ Cityscapes (67.2 mIOU, +1.4) datasets. CLUDA effectively demonstrates contrastive learning in UDA as a generic method, which can be easily integrated into any existing UDA for semantic segmentation tasks. Please refer to the supplementary material for the details on implementation.