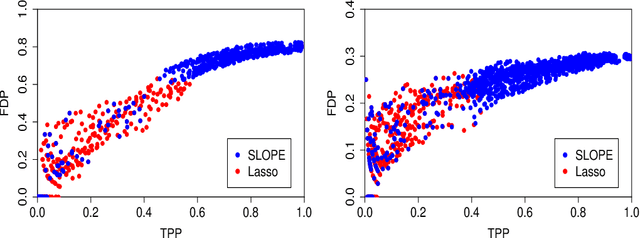
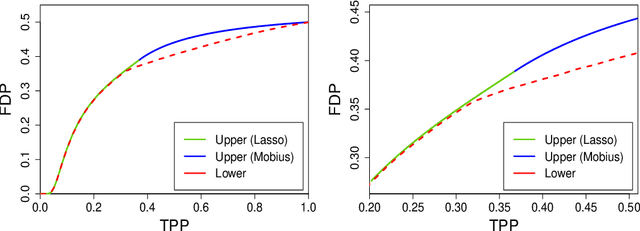
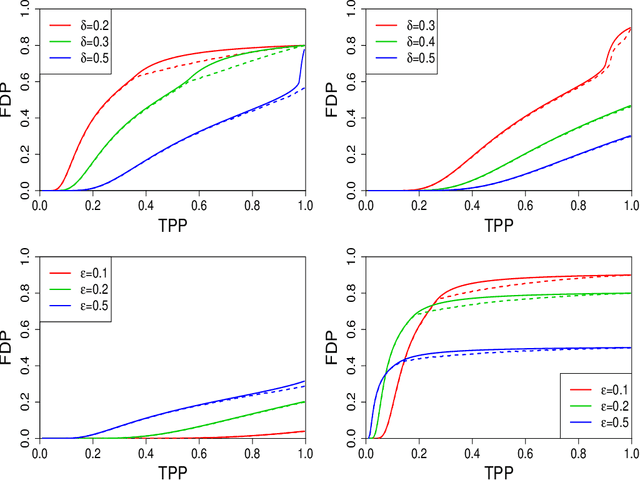
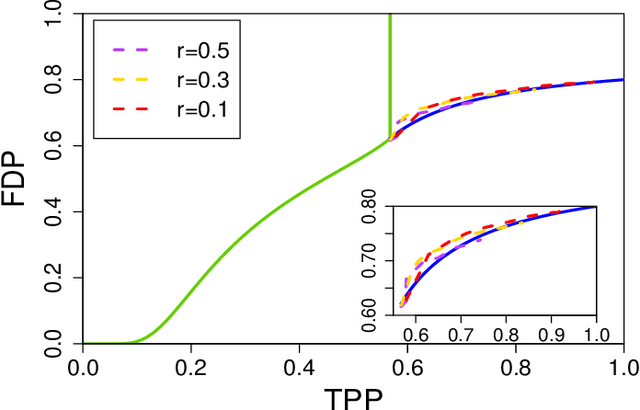
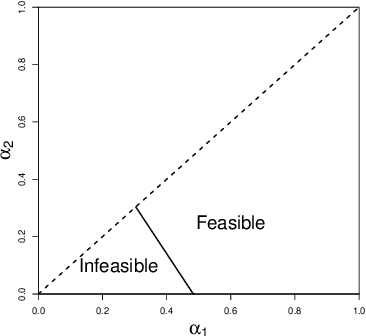
Characterizing the SLOPE Trade-off: A Variational Perspective and the Donoho-Tanner Limit

Sorted l1 regularization has been incorporated into many methods for solving high-dimensional statistical estimation problems, including the SLOPE estimator in linear regression. In this paper, we study how this relatively new regularization technique improves variable selection by characterizing the optimal SLOPE trade-off between the false discovery proportion (FDP) and true positive proportion (TPP) or, equivalently, between measures of type I error and power. Assuming a regime of linear sparsity and working under Gaussian random designs, we obtain an upper bound on the optimal trade-off for SLOPE, showing its capability of breaking the Donoho-Tanner power limit. To put it into perspective, this limit is the highest possible power that the Lasso, which is perhaps the most popular l1-based method, can achieve even with arbitrarily strong effect sizes. Next, we derive a tight lower bound that delineates the fundamental limit of sorted l1 regularization in optimally trading the FDP off for the TPP. Finally, we show that on any problem instance, SLOPE with a certain regularization sequence outperforms the Lasso, in the sense of having a smaller FDP, larger TPP and smaller l2 estimation risk simultaneously. Our proofs are based on a novel technique that reduces a variational calculus problem to a class of infinite-dimensional convex optimization problems and a very recent result from approximate message passing theory.

Algorithmic Analysis and Statistical Estimation of SLOPE via Approximate Message Passing

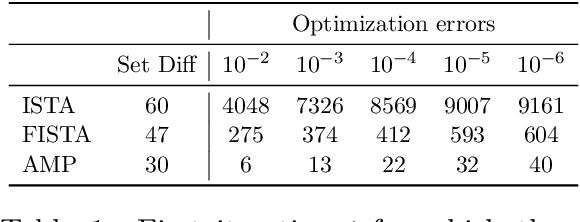
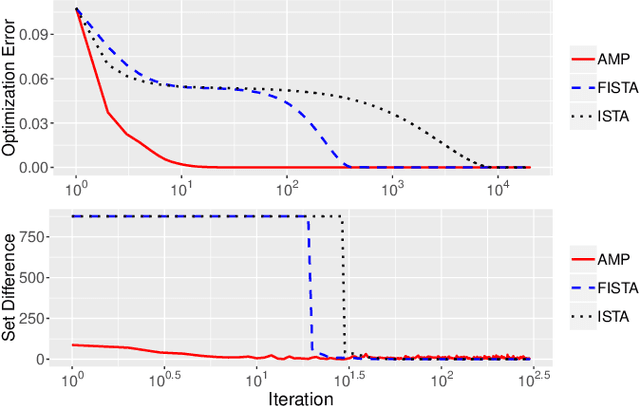
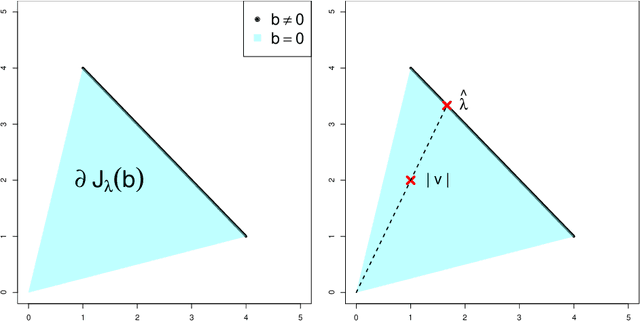
SLOPE is a relatively new convex optimization procedure for high-dimensional linear regression via the sorted l1 penalty: the larger the rank of the fitted coefficient, the larger the penalty. This non-separable penalty renders many existing techniques invalid or inconclusive in analyzing the SLOPE solution. In this paper, we develop an asymptotically exact characterization of the SLOPE solution under Gaussian random designs through solving the SLOPE problem using approximate message passing (AMP). This algorithmic approach allows us to approximate the SLOPE solution via the much more amenable AMP iterates. Explicitly, we characterize the asymptotic dynamics of the AMP iterates relying on a recently developed state evolution analysis for non-separable penalties, thereby overcoming the difficulty caused by the sorted l1 penalty. Moreover, we prove that the AMP iterates converge to the SLOPE solution in an asymptotic sense, and numerical simulations show that the convergence is surprisingly fast. Our proof rests on a novel technique that specifically leverages the SLOPE problem. In contrast to prior literature, our work not only yields an asymptotically sharp analysis but also offers an algorithmic, flexible, and constructive approach to understanding the SLOPE problem.