A Randomised Subspace Gauss-Newton Method for Nonlinear Least-Squares

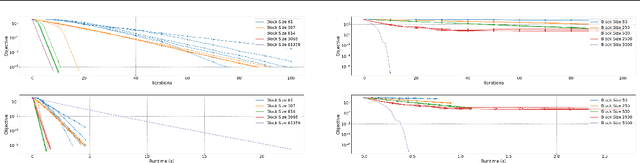
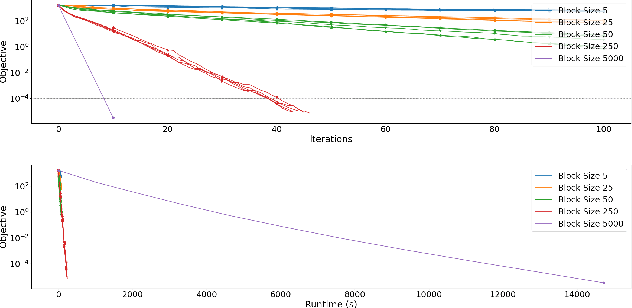
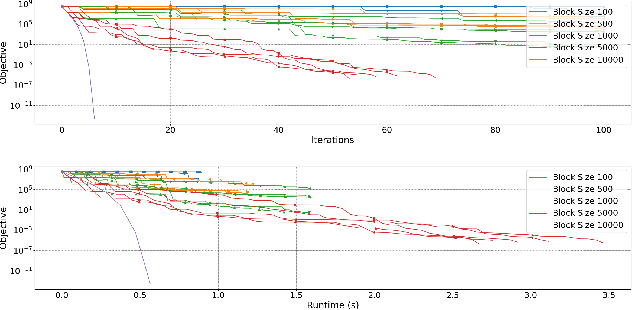
We propose a Randomised Subspace Gauss-Newton (R-SGN) algorithm for solving nonlinear least-squares optimization problems, that uses a sketched Jacobian of the residual in the variable domain and solves a reduced linear least-squares on each iteration. A sublinear global rate of convergence result is presented for a trust-region variant of R-SGN, with high probability, which matches deterministic counterpart results in the order of the accuracy tolerance. Promising preliminary numerical results are presented for R-SGN on logistic regression and on nonlinear regression problems from the CUTEst collection.

A Bayesian Network Model for Interesting Itemsets

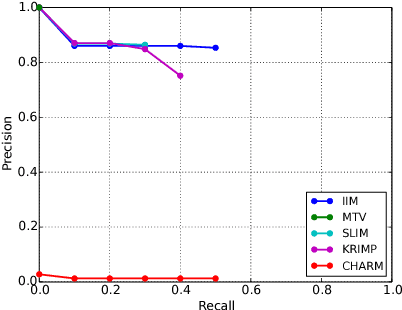
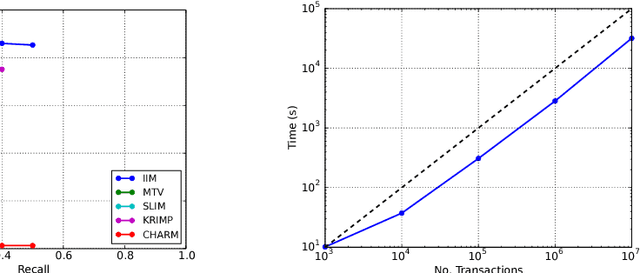
Mining itemsets that are the most interesting under a statistical model of the underlying data is a commonly used and well-studied technique for exploratory data analysis, with the most recent interestingness models exhibiting state of the art performance. Continuing this highly promising line of work, we propose the first, to the best of our knowledge, generative model over itemsets, in the form of a Bayesian network, and an associated novel measure of interestingness. Our model is able to efficiently infer interesting itemsets directly from the transaction database using structural EM, in which the E-step employs the greedy approximation to weighted set cover. Our approach is theoretically simple, straightforward to implement, trivially parallelizable and retrieves itemsets whose quality is comparable to, if not better than, existing state of the art algorithms as we demonstrate on several real-world datasets.

A Subsequence Interleaving Model for Sequential Pattern Mining

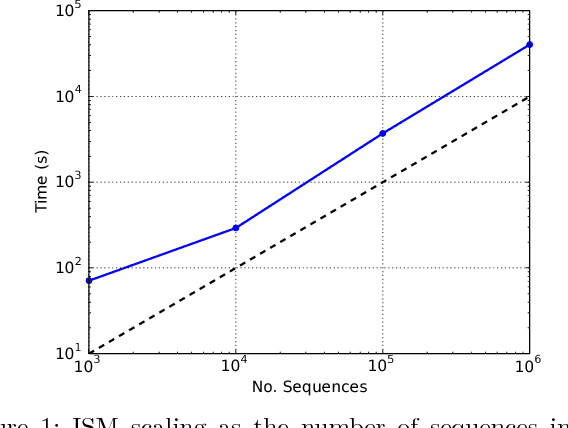
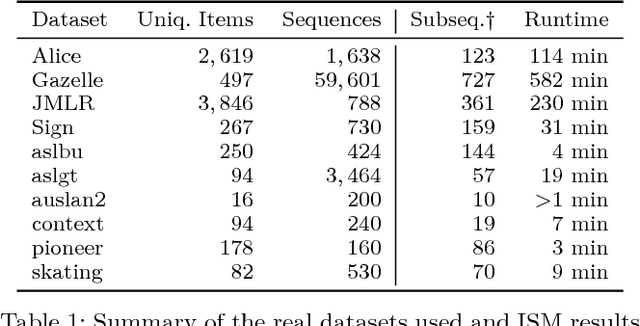
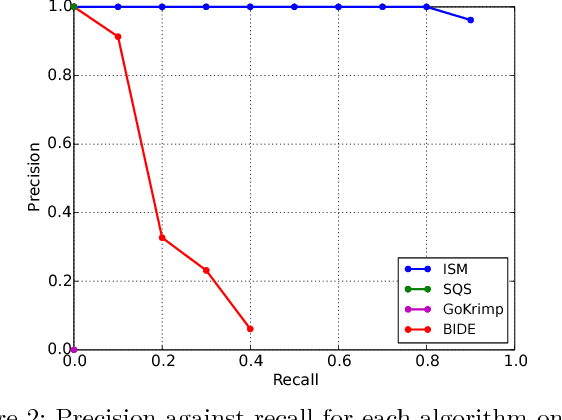
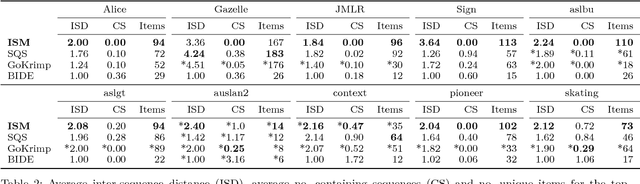
Recent sequential pattern mining methods have used the minimum description length (MDL) principle to define an encoding scheme which describes an algorithm for mining the most compressing patterns in a database. We present a novel subsequence interleaving model based on a probabilistic model of the sequence database, which allows us to search for the most compressing set of patterns without designing a specific encoding scheme. Our proposed algorithm is able to efficiently mine the most relevant sequential patterns and rank them using an associated measure of interestingness. The efficient inference in our model is a direct result of our use of a structural expectation-maximization framework, in which the expectation-step takes the form of a submodular optimization problem subject to a coverage constraint. We show on both synthetic and real world datasets that our model mines a set of sequential patterns with low spuriousness and redundancy, high interpretability and usefulness in real-world applications. Furthermore, we demonstrate that the quality of the patterns from our approach is comparable to, if not better than, existing state of the art sequential pattern mining algorithms.