Biology-inspired joint distribution neurons based on Hierarchical Correlation Reconstruction allowing for multidirectional neural networks

Popular artificial neural networks (ANN) optimize parameters for unidirectional value propagation, assuming some guessed parametrization type like Multi-Layer Perceptron (MLP) or Kolmogorov-Arnold Network (KAN). In contrast, for biological neurons e.g. "it is not uncommon for axonal propagation of action potentials to happen in both directions" \cite{axon} - suggesting they are optimized to continuously operate in multidirectional way. Additionally, statistical dependencies a single neuron could model is not just (expected) value dependence, but entire joint distributions including also higher moments. Such agnostic joint distribution neuron would allow for multidirectional propagation (of distributions or values) e.g. $\rho(x|y,z)$ or $\rho(y,z|x)$ by substituting to $\rho(x,y,z)$ and normalizing. There will be discussed Hierarchical Correlation Reconstruction (HCR) for such neuron model: assuming $\rho(x,y,z)=\sum_{ijk} a_{ijk} f_i(x) f_j(y) f_k(z)$ type parametrization of joint distribution with polynomial basis $f_i$, which allows for flexible, inexpensive processing including nonlinearities, direct model estimation and update, trained through standard backpropagation or novel ways for such structure up to tensor decomposition. Using only pairwise (input-output) dependencies, its expected value prediction becomes KAN-like with trained activation functions as polynomials, can be extended by adding higher order dependencies through included products - in conscious interpretable way, allowing for multidirectional propagation of both values and probability densities.

Extracting individual variable information for their decoupling, direct mutual information and multi-feature Granger causality

Working with multiple variables they usually contain difficult to control complex dependencies. This article proposes extraction of their individual information, e.g. $\overline{X|Y}$ as random variable containing information from $X$, but with removed information about $Y$, by using $(x,y) \leftrightarrow (\bar{x}=\textrm{CDF}_{X|Y=y}(x),y)$ reversible normalization. One application can be decoupling of individual information of variables: reversibly transform $(X_1,\ldots,X_n)\leftrightarrow(\tilde{X}_1,\ldots \tilde{X}_n)$ together containing the same information, but being independent: $\forall_{i\neq j} \tilde{X}_i\perp \tilde{X}_j, \tilde{X}_i\perp X_j$. It requires detailed models of complex conditional probability distributions - it is generally a difficult task, but here can be done through multiple dependency reducing iterations, using imperfect methods (here HCR: Hierarchical Correlation Reconstruction). It could be also used for direct mutual information - evaluating direct information transfer: without use of intermediate variables. For causality direction there is discussed multi-feature Granger causality, e.g. to trace various types of individual information transfers between such decoupled variables, including propagation time (delay).

Adaptive Student's t-distribution with method of moments moving estimator for nonstationary time series

The real life time series are usually nonstationary, bringing a difficult question of model adaptation. Classical approaches like ARMA-ARCH assume arbitrary type of dependence. To avoid such bias, we will focus on recently proposed agnostic philosophy of moving estimator: in time $t$ finding parameters optimizing e.g. $F_t=\sum_{\tau<t} (1-\eta)^{t-\tau} \ln(\rho_\theta (x_\tau))$ moving log-likelihood, evolving in time. It allows for example to estimate parameters using inexpensive exponential moving averages (EMA), like absolute central moments $E[|x-\mu|^p]$ evolving for one or multiple powers $p\in\mathbb{R}^+$ using $m_{p,t+1} = m_{p,t} + \eta (|x_t-\mu_t|^p-m_{p,t})$. Application of such general adaptive methods of moments will be presented on Student's t-distribution, popular especially in economical applications, here applied to log-returns of DJIA companies. While standard ARMA-ARCH approaches provide evolution of $\mu$ and $\sigma$, here we also get evolution of $\nu$ describing $\rho(x)\sim |x|^{-\nu-1}$ tail shape, probability of extreme events - which might turn out catastrophic, destabilizing the market.

Predicting probability distributions for cancer therapy drug selection optimization

Large variability between cell lines brings a difficult optimization problem of drug selection for cancer therapy. Standard approaches use prediction of value for this purpose, corresponding e.g. to expected value of their distribution. This article shows superiority of working on, predicting the entire probability distributions - proposing basic tools for this purpose. We are mostly interested in the best drug in their batch to be tested - proper optimization of their selection for extreme statistics requires knowledge of the entire probability distributions, which for distributions of drug properties among cell lines often turn out binomial, e.g. depending on corresponding gene. Hence for basic prediction mechanism there is proposed mixture of two Gaussians, trying to predict its weight based on additional information.

Low cost prediction of probability distributions of molecular properties for early virtual screening

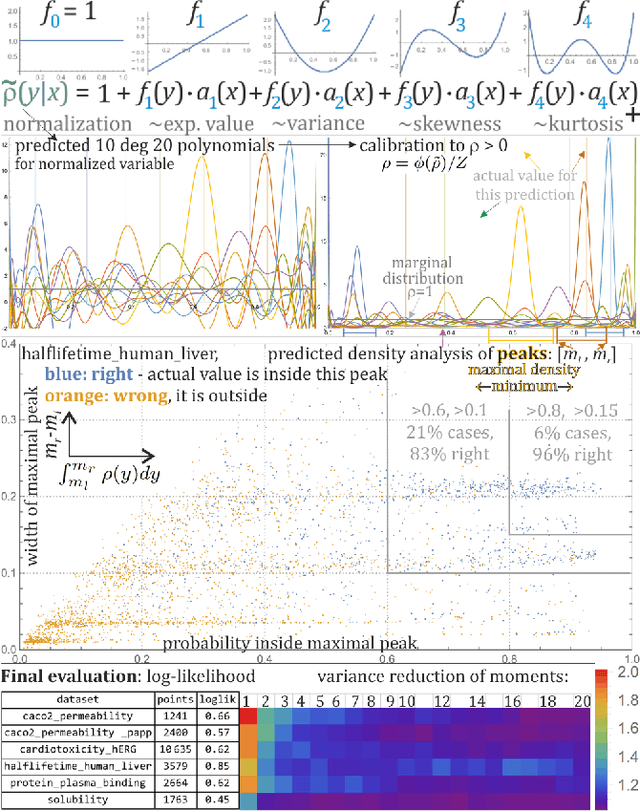
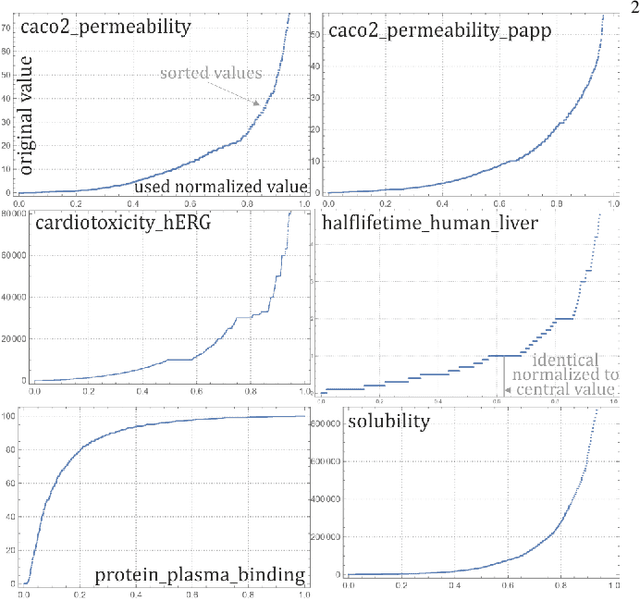
While there is a general focus on predictions of values, mathematically more appropriate is prediction of probability distributions: with additional possibilities like prediction of uncertainty, higher moments and quantiles. For the purpose of the computer-aided drug design field, this article applies Hierarchical Correlation Reconstruction approach, previously applied in the analysis of demographic, financial and astronomical data. Instead of a single linear regression to predict values, it uses multiple linear regressions to independently predict multiple moments, finally combining them into predicted probability distribution, here of several ADMET properties based on substructural fingerprint developed by Klekota\&Roth. Discussed application example is inexpensive selection of a percentage of molecules with properties nearly certain to be in a predicted or chosen range during virtual screening. Such an approach can facilitate the interpretation of the results as the predictions characterized by high rate of uncertainty are automatically detected. In addition, for each of the investigated predictive problems, we detected crucial structural features, which should be carefully considered when optimizing compounds towards particular property. The whole methodology developed in the study constitutes therefore a great support for medicinal chemists, as it enable fast rejection of compounds with the lowest potential of desired physicochemical/ADMET characteristic and guides the compound optimization process.

Predicting conditional probability distributions of redshifts of Active Galactic Nuclei using Hierarchical Correlation Reconstruction

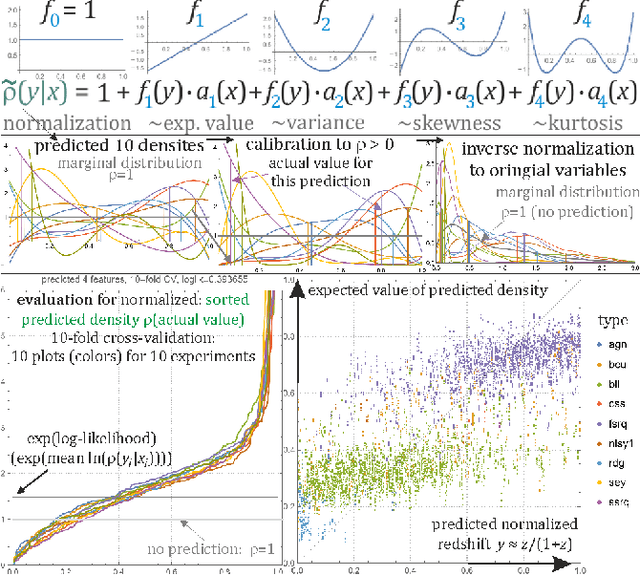
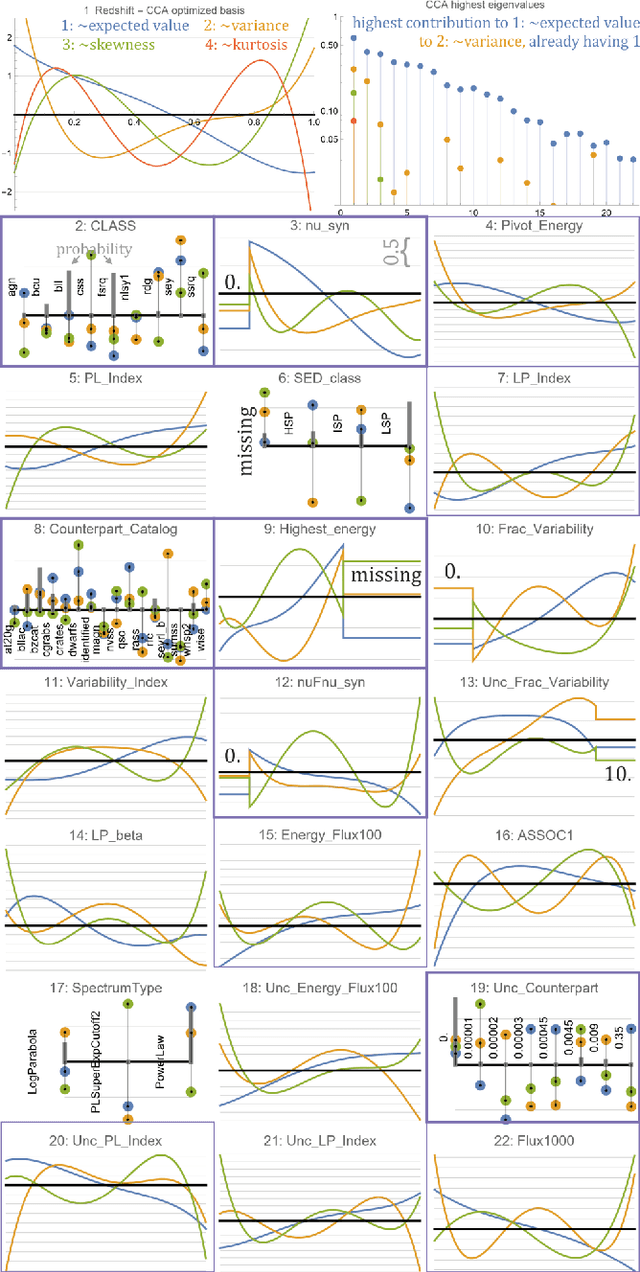
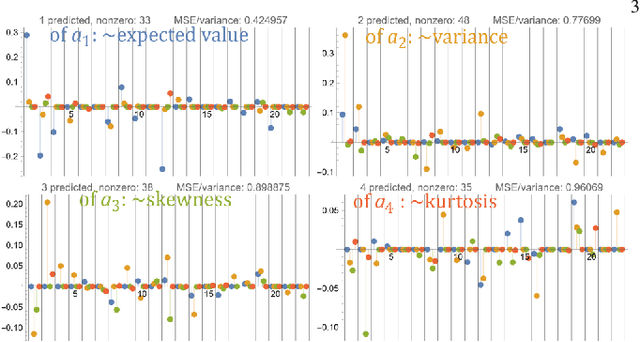
While there is a general focus on prediction of values, real data often only allows to predict conditional probability distributions, with capabilities bounded by conditional entropy $H(Y|X)$. If additionally estimating uncertainty, we can treat a predicted value as the center of Gaussian of Laplace distribution - idealization which can be far from complex conditional distributions of real data. This article applies Hierarchical Correlation Reconstruction (HCR) approach to inexpensively predict quite complex conditional probability distributions (e.g. multimodal): by independent MSE estimation of multiple moment-like parameters, which allow to reconstruct the conditional distribution. Using linear regression for this purpose, we get interpretable models: with coefficients describing contributions of features to conditional moments. This article extends on the original approach especially by using Canonical Correlation Analysis (CCA) for feature optimization and l1 "lasso" regularization, focusing on practical problem of prediction of redshift of Active Galactic Nuclei (AGN) based on Fourth Fermi-LAT Data Release 2 (4LAC) dataset.

Fast optimization of common basis for matrix set through Common Singular Value Decomposition

SVD (singular value decomposition) is one of the basic tools of machine learning, allowing to optimize basis for a given matrix. However, sometimes we have a set of matrices $\{A_k\}_k$ instead, and would like to optimize a single common basis for them: find orthogonal matrices $U$, $V$, such that $\{U^T A_k V\}$ set of matrices is somehow simpler. For example DCT-II is orthonormal basis of functions commonly used in image/video compression - as discussed here, this kind of basis can be quickly automatically optimized for a given dataset. While also discussed gradient descent optimization might be computationally costly, there is proposed CSVD (common SVD): fast general approach based on SVD. Specifically, we choose $U$ as built of eigenvectors of $\sum_i (w_k)^q (A_k A_k^T)^p$ and $V$ of $\sum_k (w_k)^q (A_k^T A_k)^p$, where $w_k$ are their weights, $p,q>0$ are some chosen powers e.g. 1/2, optionally with normalization e.g. $A \to A - rc^T$ where $r_i=\sum_j A_{ij}, c_j =\sum_i A_{ij}$.

Exploiting context dependence for image compression with upsampling

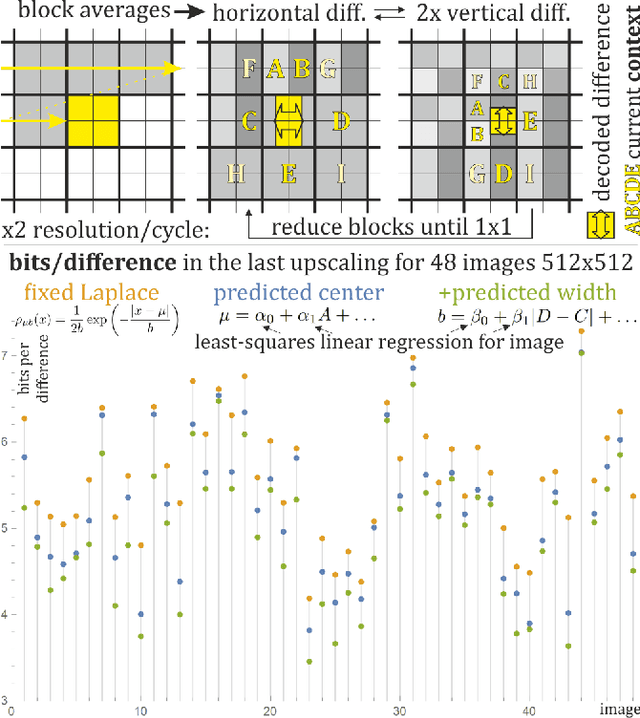
Image compression with upsampling encodes information to succeedingly increase image resolution, for example by encoding differences in FUIF and JPEG XL. It is useful for progressive decoding, also often can improve compression ratio. However, the currently used solutions rather do not exploit context dependence for encoding of such upscaling information. This article discusses simple inexpensive general techniques for this purpose, which allowed to save on average 0.645 bits/difference (between 0.138 and 1.489) for the last upscaling for 48 standard $512\times 512$ grayscale images - compared to assumption of fixed Laplace distribution. Using least squares linear regression of context to predict center of Laplace distribution gave on average 0.393 bits/difference savings. The remaining savings were obtained by additionally predicting width of this Laplace distribution, also using just the least squares linear regression. The presented simple inexpensive general methodology can be also used for different types of data like DCT coefficients in lossy image compression.

Adaptive exponential power distribution with moving estimator for nonstationary time series

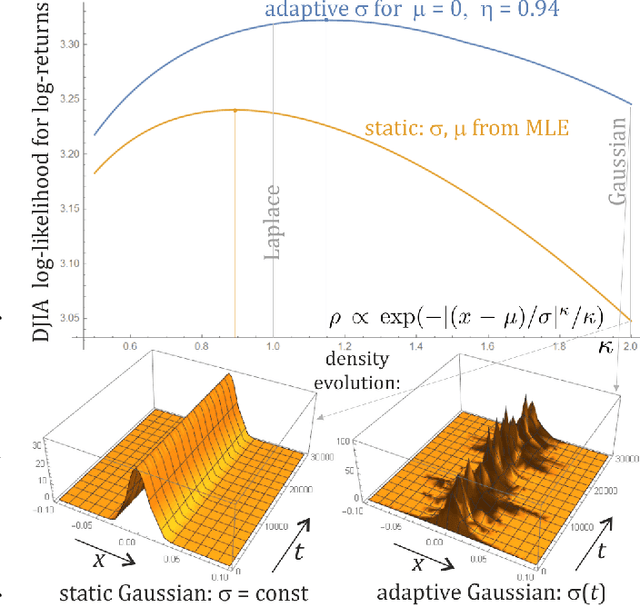
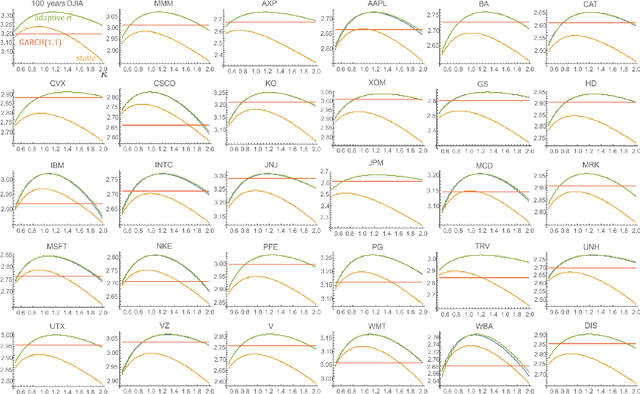
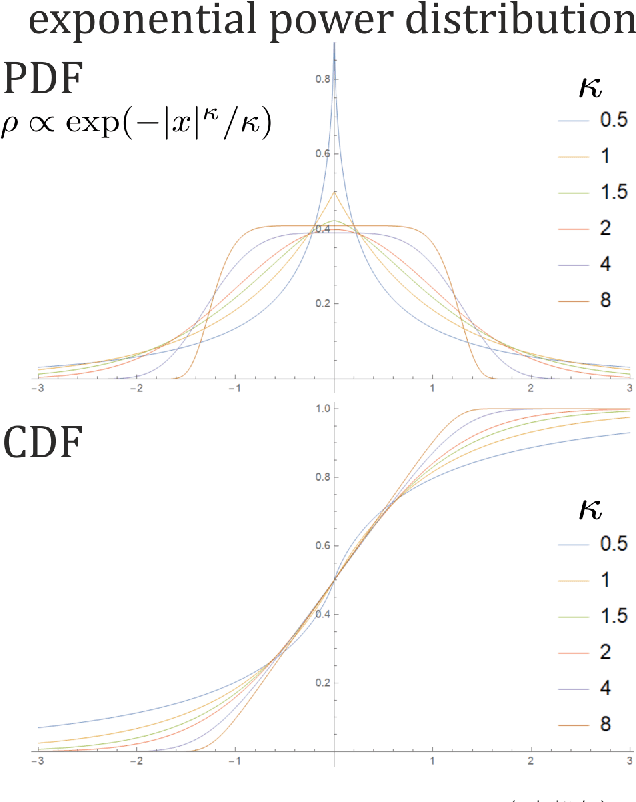
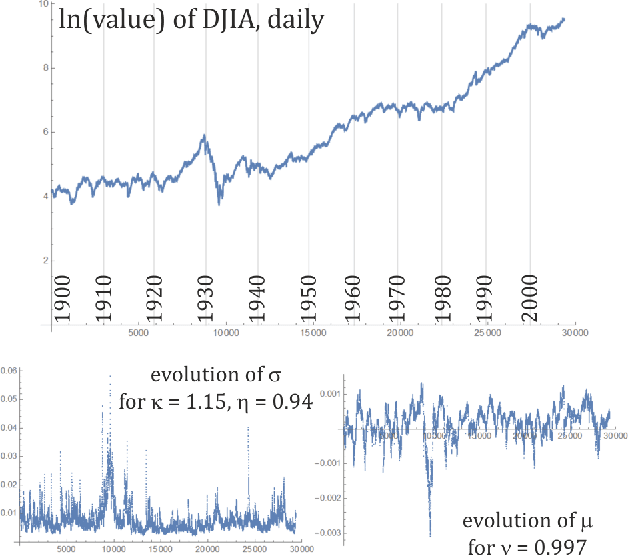
While standard estimation assumes that all datapoints are from probability distribution of the same fixed parameters $\theta$, we will focus on maximum likelihood (ML) adaptive estimation for nonstationary time series: separately estimating parameters $\theta_T$ for each time $T$ based on the earlier values $(x_t)_{t<T}$ using (exponential) moving ML estimator $\theta_T=\arg\max_\theta l_T$ for $l_T=\sum_{t<T} \eta^{T-t} \ln(\rho_\theta (x_t))$ and some $\eta\in(0,1]$. Computational cost of such moving estimator is generally much higher as we need to optimize log-likelihood multiple times, however, in many cases it can be made inexpensive thanks to dependencies. We focus on such example: $\rho(x)\propto \exp(-|(x-\mu)/\sigma|^\kappa/\kappa)$ exponential power distribution (EPD) family, which covers wide range of tail behavior like Gaussian ($\kappa=2$) or Laplace ($\kappa=1$) distribution. It is also convenient for such adaptive estimation of scale parameter $\sigma$ as its standard ML estimation is $\sigma^\kappa$ being average $\|x-\mu\|^\kappa$. By just replacing average with exponential moving average: $(\sigma_{T+1})^\kappa=\eta(\sigma_T)^\kappa +(1-\eta)|x_T-\mu|^\kappa$ we can inexpensively make it adaptive. It is tested on daily log-return series for DJIA companies, leading to essentially better log-likelihoods than standard (static) estimation, with optimal $\kappa$ tails types varying between companies. Presented general alternative estimation philosophy provides tools which might be useful for building better models for analysis of nonstationary time-series.

SGD momentum optimizer with step estimation by online parabola model

In stochastic gradient descent, especially for neural network training, there are currently dominating first order methods: not modeling local distance to minimum. This information required for optimal step size is provided by second order methods, however, they have many difficulties, starting with full Hessian having square of dimension number of coefficients. This article proposes a minimal step from successful first order momentum method toward second order: online parabola modelling in just a single direction: normalized $\hat{v}$ from momentum method. It is done by estimating linear trend of gradients $\vec{g}=\nabla F(\vec{\theta})$ in $\hat{v}$ direction: such that $g(\vec{\theta}_\bot+\theta\hat{v})\approx \lambda (\theta -p)$ for $\theta = \vec{\theta}\cdot \hat{v}$, $g= \vec{g}\cdot \hat{v}$, $\vec{\theta}_\bot=\vec{\theta}-\theta\hat{v}$. Using linear regression, $\lambda$, $p$ are MSE estimated by just updating four averages (of $g$, $\theta$, $g\theta$, $\theta^2$) in the considered direction. Exponential moving averages allow here for inexpensive online estimation, weakening contribution of the old gradients. Controlling sign of curvature $\lambda$, we can repel from saddles in contrast to attraction in standard Newton method. In the remaining directions: not considered in second order model, we can simultaneously perform e.g. gradient descent.