Exploiting context dependence for image compression with upsampling

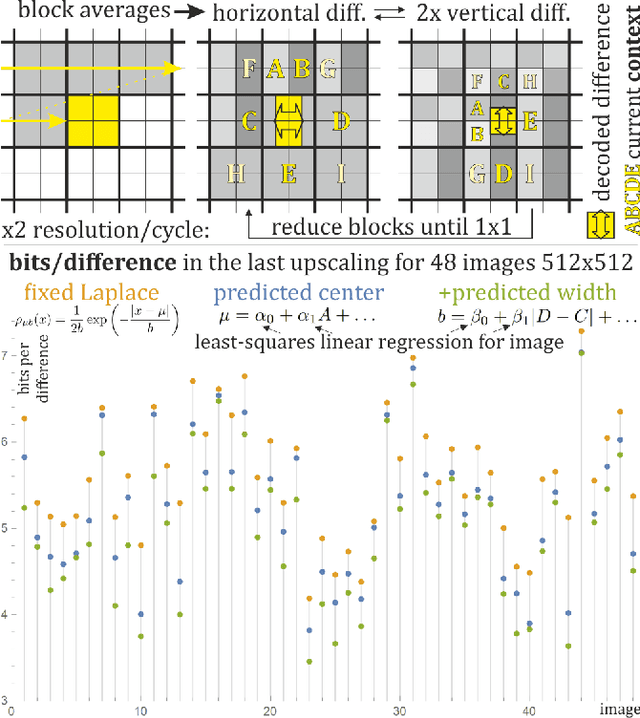
Image compression with upsampling encodes information to succeedingly increase image resolution, for example by encoding differences in FUIF and JPEG XL. It is useful for progressive decoding, also often can improve compression ratio. However, the currently used solutions rather do not exploit context dependence for encoding of such upscaling information. This article discusses simple inexpensive general techniques for this purpose, which allowed to save on average 0.645 bits/difference (between 0.138 and 1.489) for the last upscaling for 48 standard $512\times 512$ grayscale images - compared to assumption of fixed Laplace distribution. Using least squares linear regression of context to predict center of Laplace distribution gave on average 0.393 bits/difference savings. The remaining savings were obtained by additionally predicting width of this Laplace distribution, also using just the least squares linear regression. The presented simple inexpensive general methodology can be also used for different types of data like DCT coefficients in lossy image compression.