Adaptive exponential power distribution with moving estimator for nonstationary time series
Paper and Code
Mar 23, 2020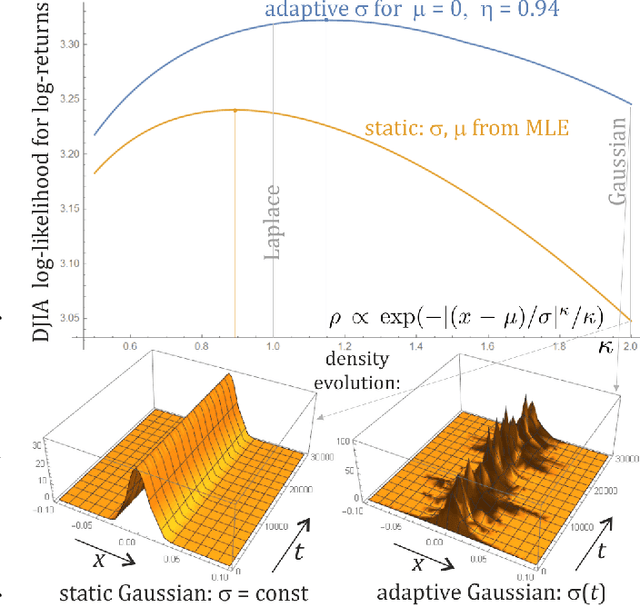
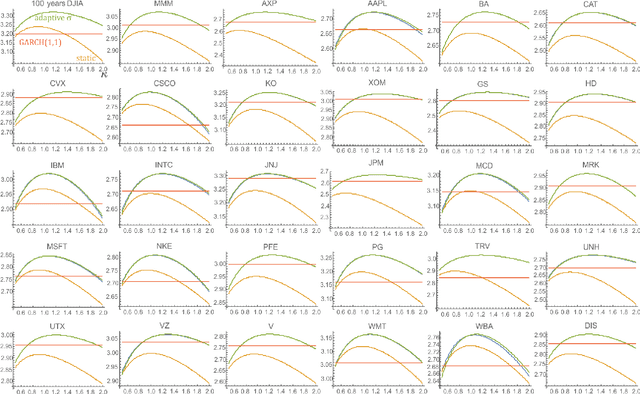
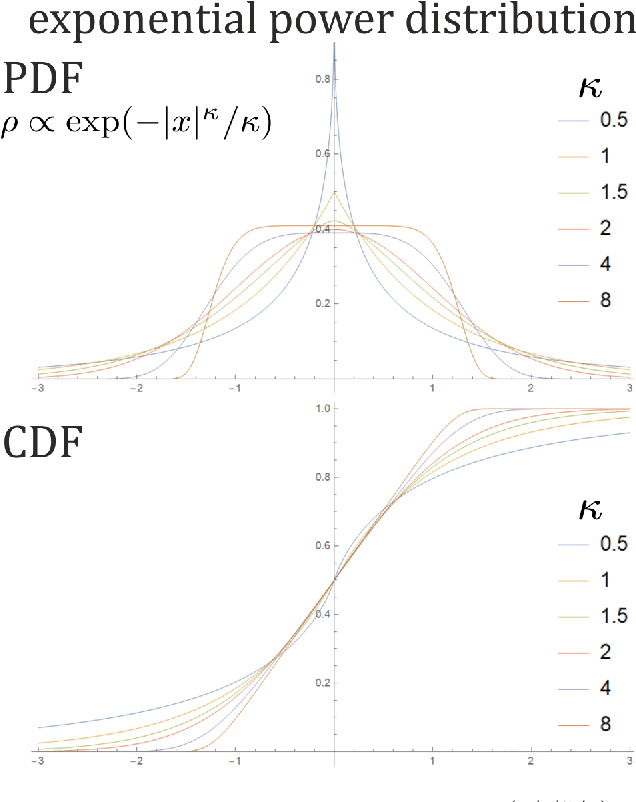
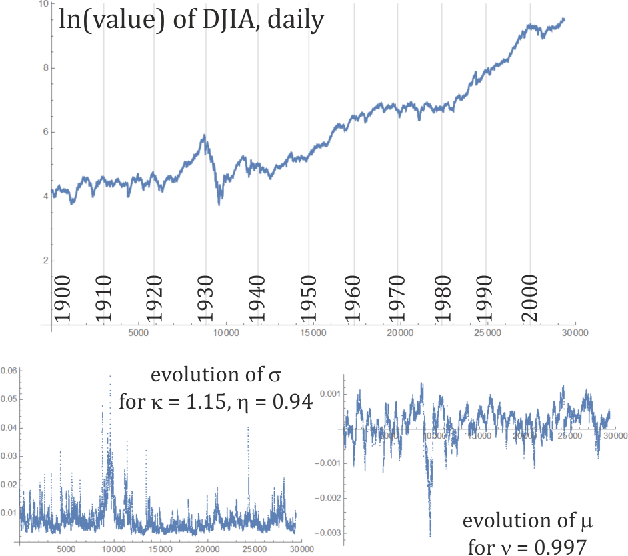
While standard estimation assumes that all datapoints are from probability distribution of the same fixed parameters $\theta$, we will focus on maximum likelihood (ML) adaptive estimation for nonstationary time series: separately estimating parameters $\theta_T$ for each time $T$ based on the earlier values $(x_t)_{t<T}$ using (exponential) moving ML estimator $\theta_T=\arg\max_\theta l_T$ for $l_T=\sum_{t<T} \eta^{T-t} \ln(\rho_\theta (x_t))$ and some $\eta\in(0,1]$. Computational cost of such moving estimator is generally much higher as we need to optimize log-likelihood multiple times, however, in many cases it can be made inexpensive thanks to dependencies. We focus on such example: $\rho(x)\propto \exp(-|(x-\mu)/\sigma|^\kappa/\kappa)$ exponential power distribution (EPD) family, which covers wide range of tail behavior like Gaussian ($\kappa=2$) or Laplace ($\kappa=1$) distribution. It is also convenient for such adaptive estimation of scale parameter $\sigma$ as its standard ML estimation is $\sigma^\kappa$ being average $\|x-\mu\|^\kappa$. By just replacing average with exponential moving average: $(\sigma_{T+1})^\kappa=\eta(\sigma_T)^\kappa +(1-\eta)|x_T-\mu|^\kappa$ we can inexpensively make it adaptive. It is tested on daily log-return series for DJIA companies, leading to essentially better log-likelihoods than standard (static) estimation, with optimal $\kappa$ tails types varying between companies. Presented general alternative estimation philosophy provides tools which might be useful for building better models for analysis of nonstationary time-series.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge