A Physics-informed Deep Learning Approach for Minimum Effort Stochastic Control of Colloidal Self-Assembly

We propose formulating the finite-horizon stochastic optimal control problem for colloidal self-assembly in the space of probability density functions (PDFs) of the underlying state variables (namely, order parameters). The control objective is formulated in terms of steering the state PDFs from a prescribed initial probability measure towards a prescribed terminal probability measure with minimum control effort. For specificity, we use a univariate stochastic state model from the literature. Both the analysis and the computational steps for control synthesis as developed in this paper generalize for multivariate stochastic state dynamics given by generic nonlinear in state and non-affine in control models. We derive the conditions of optimality for the associated optimal control problem. This derivation yields a system of three coupled partial differential equations together with the boundary conditions at the initial and terminal times. The resulting system is a generalized instance of the so-called Schr\"{o}dinger bridge problem. We then determine the optimal control policy by training a physics-informed deep neural network, where the "physics" are the derived conditions of optimality. The performance of the proposed solution is demonstrated via numerical simulations on a benchmark colloidal self-assembly problem.

Stochastic Physics-Informed Neural Networks (SPINN): A Moment-Matching Framework for Learning Hidden Physics within Stochastic Differential Equations

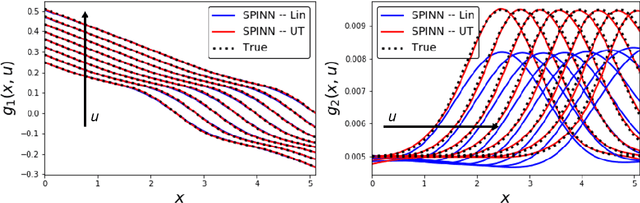
Stochastic differential equations (SDEs) are used to describe a wide variety of complex stochastic dynamical systems. Learning the hidden physics within SDEs is crucial for unraveling fundamental understanding of the stochastic and nonlinear behavior of these systems. We propose a flexible and scalable framework for training deep neural networks to learn constitutive equations that represent hidden physics within SDEs. The proposed stochastic physics-informed neural network framework (SPINN) relies on uncertainty propagation and moment-matching techniques along with state-of-the-art deep learning strategies. SPINN first propagates stochasticity through the known structure of the SDE (i.e., the known physics) to predict the time evolution of statistical moments of the stochastic states. SPINN learns (deep) neural network representations of the hidden physics by matching the predicted moments to those estimated from data. Recent advances in automatic differentiation and mini-batch gradient descent are leveraged to establish the unknown parameters of the neural networks. We demonstrate SPINN on three benchmark in-silico case studies and analyze the framework's robustness and numerical stability. SPINN provides a promising new direction for systematically unraveling the hidden physics of multivariate stochastic dynamical systems with multiplicative noise.