Some Might Say All You Need Is Sum

The expressivity of Graph Neural Networks (GNNs) is dependent on the aggregation functions they employ. Theoretical works have pointed towards Sum aggregation GNNs subsuming every other GNNs, while certain practical works have observed a clear advantage to using Mean and Max. An examination of the theoretical guarantee identifies two caveats. First, it is size-restricted, that is, the power of every specific GNN is limited to graphs of a certain maximal size. Successfully processing larger graphs may require an other GNN, and so on. Second, it concerns the power to distinguish non-isomorphic graphs, not the power to approximate general functions on graphs, and the former does not necessarily imply the latter. It is important that a GNN's usability will not be limited to graphs of any certain maximal size. Therefore, we explore the realm of unrestricted-size expressivity. We prove that simple functions, which can be computed exactly by Mean or Max GNNs, are inapproximable by any Sum GNN. We prove that under certain restrictions, every Mean or Max GNNs can be approximated by a Sum GNN, but even there, a combination of (Sum, [Mean/Max]) is more expressive than Sum alone. Lastly, we prove further expressivity limitations of Sum-GNNs.

Graph Learning with 1D Convolutions on Random Walks

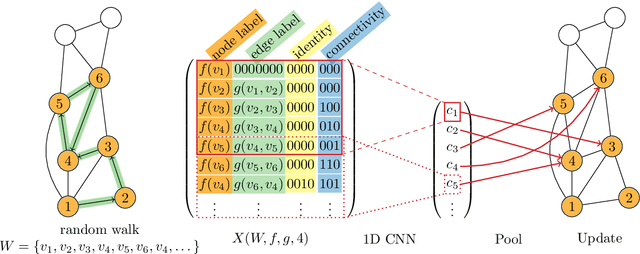
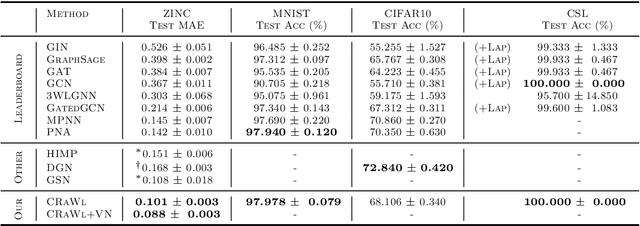
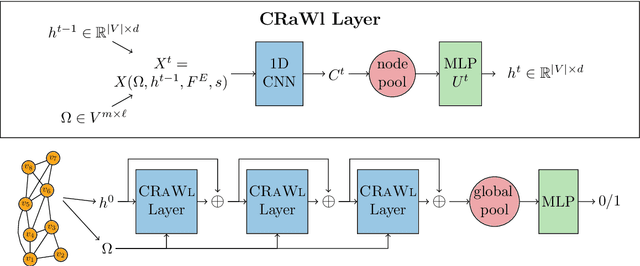
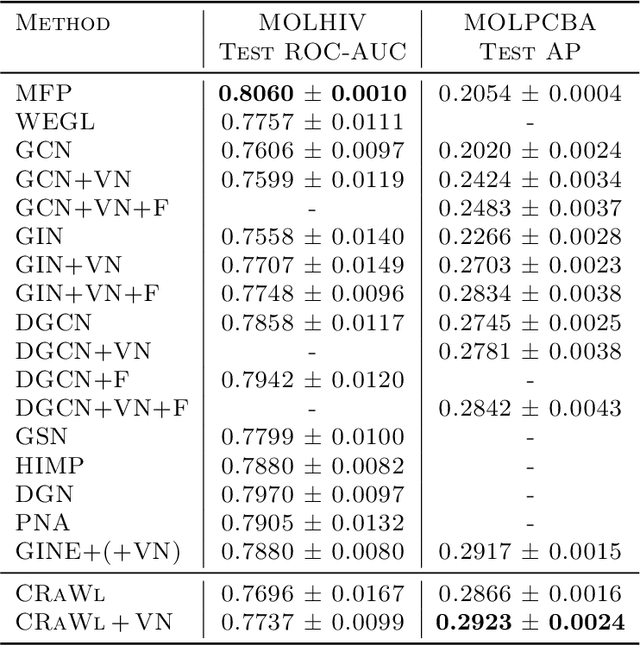
We propose CRaWl (CNNs for Random Walks), a novel neural network architecture for graph learning. It is based on processing sequences of small subgraphs induced by random walks with standard 1D CNNs. Thus, CRaWl is fundamentally different from typical message passing graph neural network architectures. It is inspired by techniques counting small subgraphs, such as the graphlet kernel and motif counting, and combines them with random walk based techniques in a highly efficient and scalable neural architecture. We demonstrate empirically that CRaWl matches or outperforms state-of-the-art GNN architectures across a multitude of benchmark datasets for graph learning.

RUN-CSP: Unsupervised Learning of Message Passing Networks for Binary Constraint Satisfaction Problems

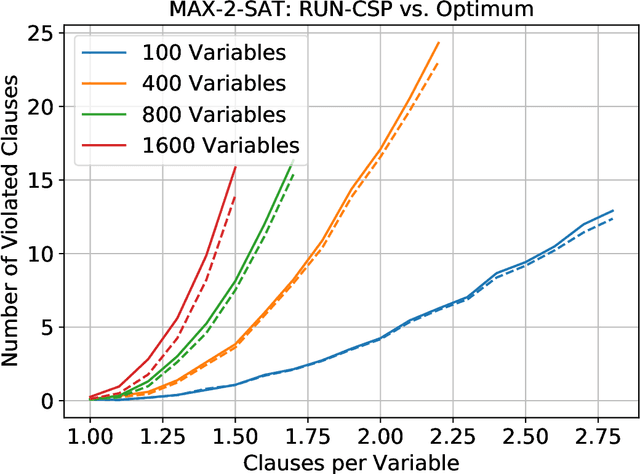
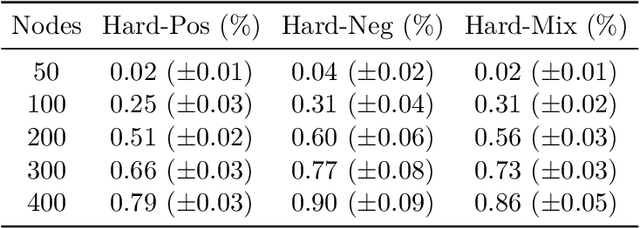
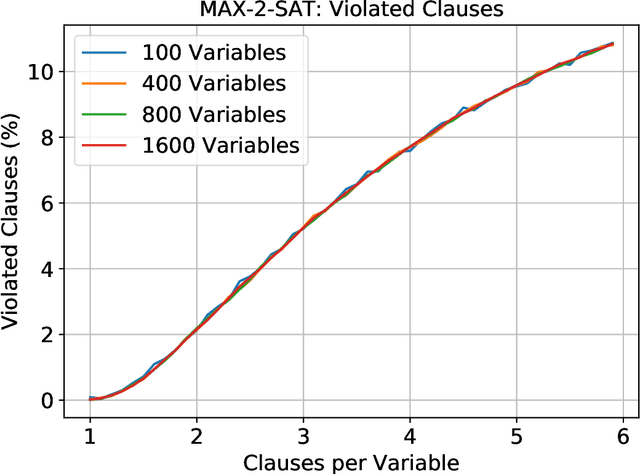
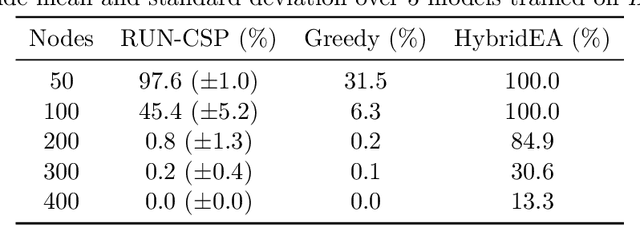
Constraint satisfaction problems form an important and wide class of combinatorial search and optimization problems with many applications in AI and other areas. We introduce a recurrent neural network architecture RUN-CSP (Recurrent Unsupervised Neural Network for Constraint Satisfaction Problems) to train message passing networks solving binary constraint satisfaction problems (CSPs) or their optimization versions (Max-CSP). The architecture is universal in the sense that it works for all binary CSPs: depending on the constraint language, we can automtically design a loss function, which is then used to train generic neural nets. In this paper, we experimentally evaluate our approach for the 3-colorability problem (3-Col) and its optimization version (Max-3-Col) and for the maximum 2-satisfiability problem (Max-2-Sat). We also extend the framework to work for related optimization problems such as the maximum independent set problem (Max-IS). Training is unsupervised, we train the network on arbitrary (unlabeled) instances of the problems. Moreover, we experimentally show that it suffices to train on relatively small instances; the resulting message passing network will perform well on much larger instances (at least 10-times larger).