RUN-CSP: Unsupervised Learning of Message Passing Networks for Binary Constraint Satisfaction Problems

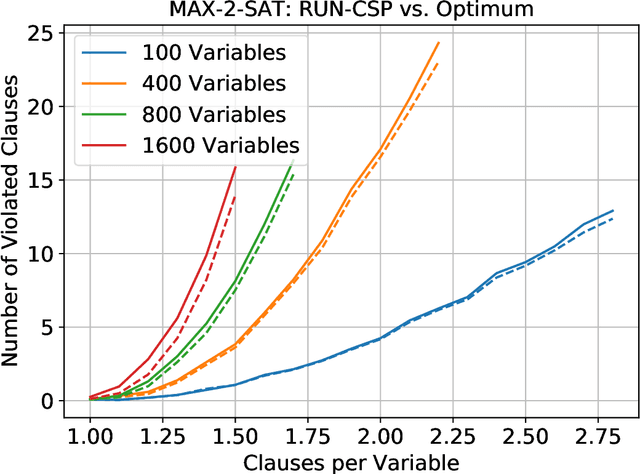
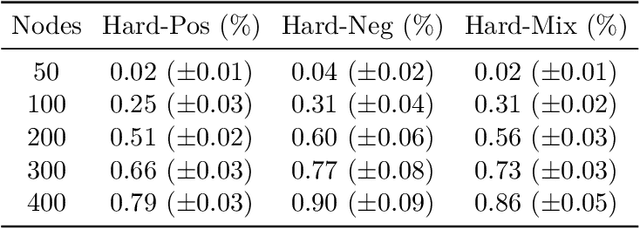
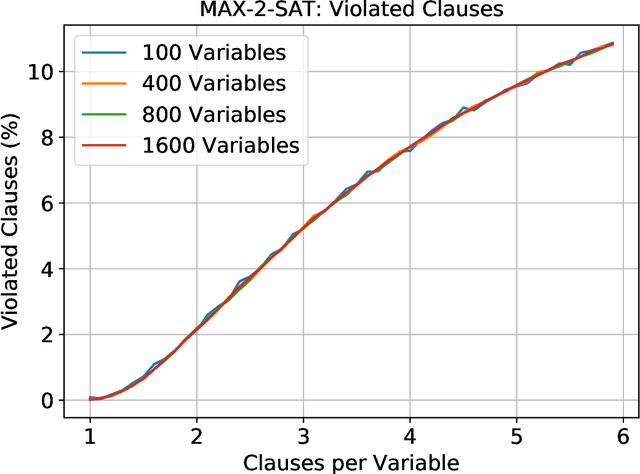
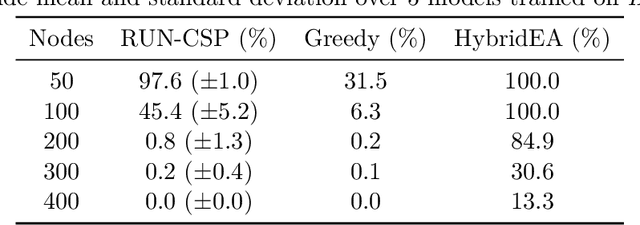
Constraint satisfaction problems form an important and wide class of combinatorial search and optimization problems with many applications in AI and other areas. We introduce a recurrent neural network architecture RUN-CSP (Recurrent Unsupervised Neural Network for Constraint Satisfaction Problems) to train message passing networks solving binary constraint satisfaction problems (CSPs) or their optimization versions (Max-CSP). The architecture is universal in the sense that it works for all binary CSPs: depending on the constraint language, we can automtically design a loss function, which is then used to train generic neural nets. In this paper, we experimentally evaluate our approach for the 3-colorability problem (3-Col) and its optimization version (Max-3-Col) and for the maximum 2-satisfiability problem (Max-2-Sat). We also extend the framework to work for related optimization problems such as the maximum independent set problem (Max-IS). Training is unsupervised, we train the network on arbitrary (unlabeled) instances of the problems. Moreover, we experimentally show that it suffices to train on relatively small instances; the resulting message passing network will perform well on much larger instances (at least 10-times larger).