Resource recommender system performance improvement by exploring similar tags and detecting tags communities

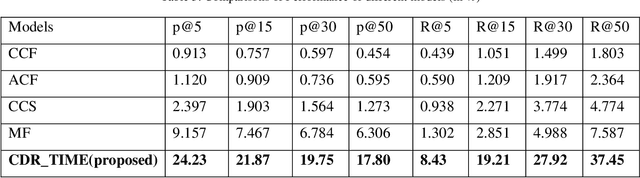
Many researchers have used tag information to improve the performance of recommendation techniques in recommender systems. Examining the tags of users will help to get their interests and leads to more accuracy in the recommendations. Since user-defined tags are chosen freely and without any restrictions, problems arise in determining their exact meaning and the similarity of tags. On the other hand, using thesauruses and ontologies to find the meaning of tags is not very efficient due to their free definition by users and the use of different languages in many data sets. Therefore, this article uses the mathematical and statistical methods to determine lexical similarity and co-occurrence tags solution to assign semantic similarity. On the other hand, due to the change of users' interests over time this article have considered the time of tag assignments in co-occurrence tags for determined similarity of tags. Then the graph is created based on these similarities. For modeling the interests of the users, the communities of tags are determined by using community detection methods. So recommendations based on the communities of tags and similarity between resources are done. The performance of the proposed method has been done using two criteria of precision and recall based on evaluations with "Delicious" dataset. The evaluation results show that, the precision and recall of the proposed method have significantly improved, compared to the other methods.

The Application of Imperialist Competitive Algorithm for Fuzzy Random Portfolio Selection Problem

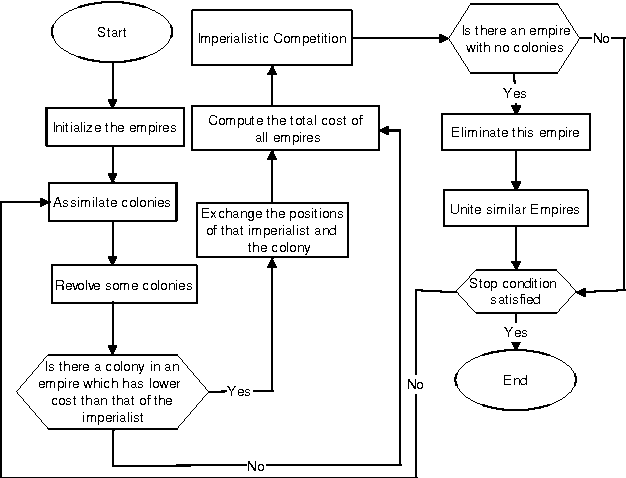
This paper presents an implementation of the Imperialist Competitive Algorithm (ICA) for solving the fuzzy random portfolio selection problem where the asset returns are represented by fuzzy random variables. Portfolio Optimization is an important research field in modern finance. By using the necessity-based model, fuzzy random variables reformulate to the linear programming and ICA will be designed to find the optimum solution. To show the efficiency of the proposed method, a numerical example illustrates the whole idea on implementation of ICA for fuzzy random portfolio selection problem.