Adaptive Off-Policy Inference for M-Estimators Under Model Misspecification

When data are collected adaptively, such as in bandit algorithms, classical statistical approaches such as ordinary least squares and $M$-estimation will often fail to achieve asymptotic normality. Although recent lines of work have modified the classical approaches to ensure valid inference on adaptively collected data, most of these works assume that the model is correctly specified. We propose a method that provides valid inference for M-estimators that use adaptively collected bandit data with a (possibly) misspecified working model. A key ingredient in our approach is the use of flexible machine learning approaches to stabilize the variance induced by adaptive data collection. A major novelty is that our procedure enables the construction of valid confidence sets even in settings where treatment policies are unstable and non-converging, such as when there is no unique optimal arm and standard bandit algorithms are used. Empirical results on semi-synthetic datasets constructed from the Osteoarthritis Initiative demonstrate that the method maintains type I error control, while existing methods for inference in adaptive settings do not cover in the misspecified case.

Data blurring: sample splitting a single sample

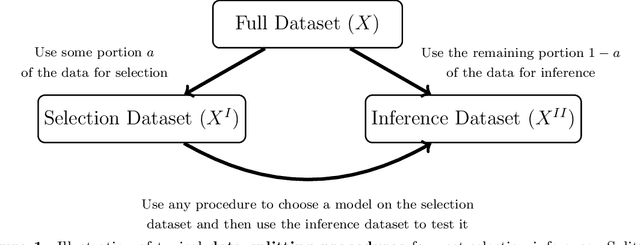
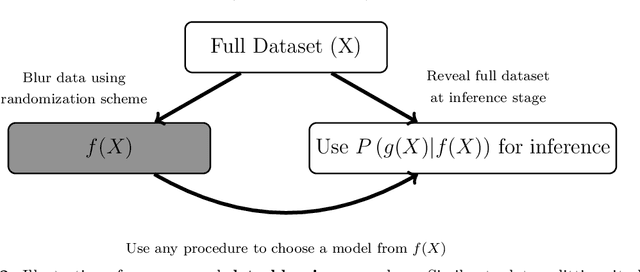
Suppose we observe a random vector $X$ from some distribution $P$ in a known family with unknown parameters. We ask the following question: when is it possible to split $X$ into two parts $f(X)$ and $g(X)$ such that neither part is sufficient to reconstruct $X$ by itself, but both together can recover $X$ fully, and the joint distribution of $(f(X),g(X))$ is tractable? As one example, if $X=(X_1,\dots,X_n)$ and $P$ is a product distribution, then for any $m<n$, we can split the sample to define $f(X)=(X_1,\dots,X_m)$ and $g(X)=(X_{m+1},\dots,X_n)$. Rasines and Young (2021) offers an alternative route of accomplishing this task through randomization of $X$ with additive Gaussian noise which enables post-selection inference in finite samples for Gaussian distributed data and asymptotically for non-Gaussian additive models. In this paper, we offer a more general methodology for achieving such a split in finite samples by borrowing ideas from Bayesian inference to yield a (frequentist) solution that can be viewed as a continuous analog of data splitting. We call our method data blurring, as an alternative to data splitting, data carving and p-value masking. We exemplify the method on a few prototypical applications, such as post-selection inference for trend filtering and other regression problems.