Bayesian Screening: Multi-test Bayesian Optimization Applied to in silico Material Screening

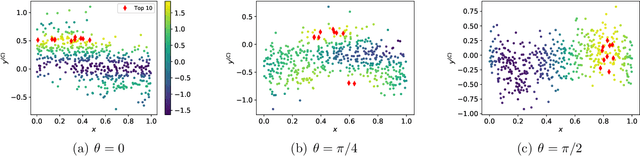
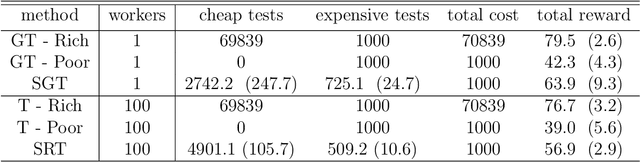
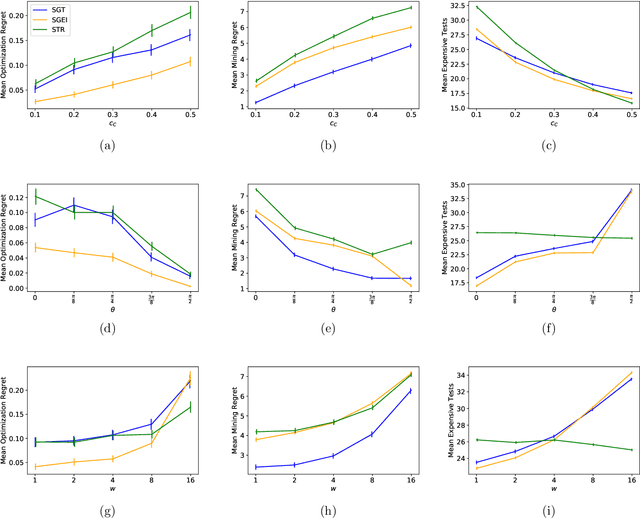
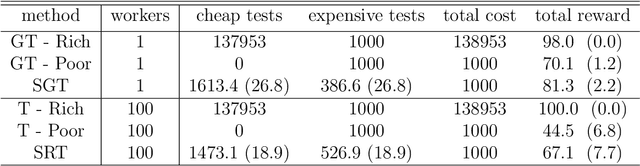
We present new multi-test Bayesian optimization models and algorithms for use in large scale material screening applications. Our screening problems are designed around two tests, one expensive and one cheap. This paper differs from other recent work on multi-test Bayesian optimization through use of a flexible model that allows for complex, non-linear relationships between the cheap and expensive test scores. This additional modeling flexibility is essential in the material screening applications which we describe. We demonstrate the power of our new algorithms on a family of synthetic toy problems as well as on real data from two large scale screening studies.

Latitude: A Model for Mixed Linear-Tropical Matrix Factorization

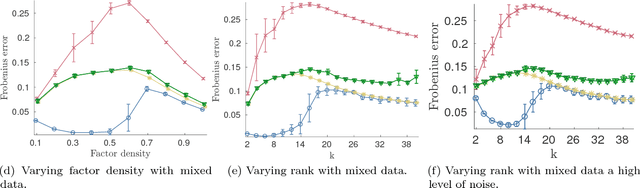
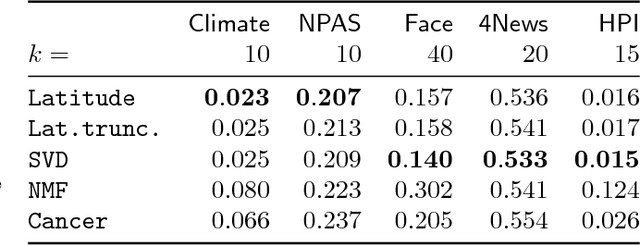
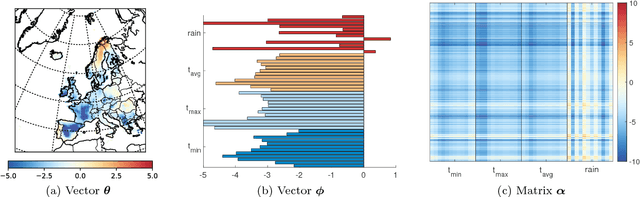
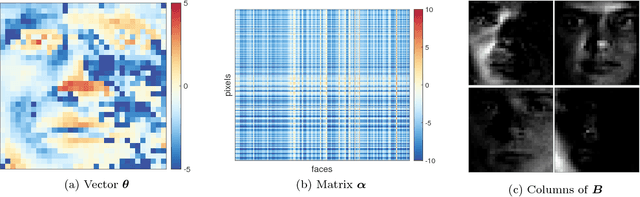
Nonnegative matrix factorization (NMF) is one of the most frequently-used matrix factorization models in data analysis. A significant reason to the popularity of NMF is its interpretability and the `parts of whole' interpretation of its components. Recently, max-times, or subtropical, matrix factorization (SMF) has been introduced as an alternative model with equally interpretable `winner takes it all' interpretation. In this paper we propose a new mixed linear--tropical model, and a new algorithm, called Latitude, that combines NMF and SMF, being able to smoothly alternate between the two. In our model, the data is modeled using the latent factors and latent parameters that control whether the factors are interpreted as NMF or SMF features, or their mixtures. We present an algorithm for our novel matrix factorization. Our experiments show that our algorithm improves over both baselines, and can yield interpretable results that reveal more of the latent structure than either NMF or SMF alone.

Max-plus statistical leverage scores

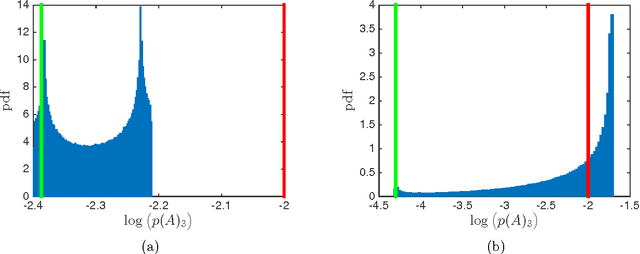
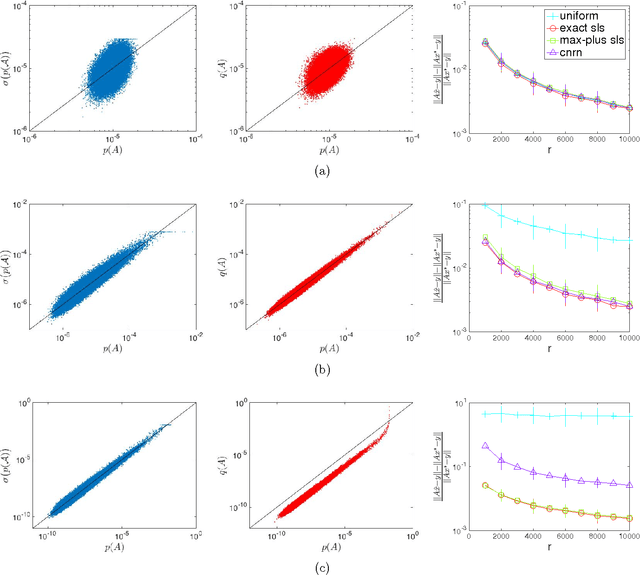
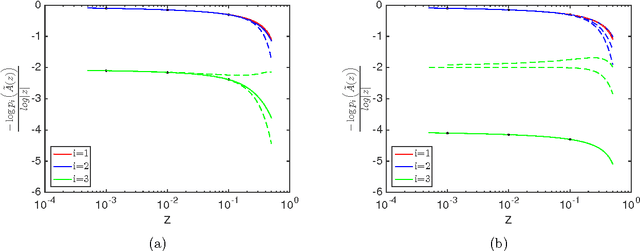
The statistical leverage scores of a complex matrix $A\in\mathbb{C}^{n\times d}$ record the degree of alignment between col$(A)$ and the coordinate axes in $\mathbb{C}^n$. These score are used in random sampling algorithms for solving certain numerical linear algebra problems. In this paper we present a max-plus algebraic analogue for statistical leverage scores. We show that max-plus statistical leverage scores can be used to calculate the exact asymptotic behavior of the conventional statistical leverage scores of a generic matrices of Puiseux series and also provide a novel way to approximate the conventional statistical leverage scores of a fixed or complex matrix. The advantage of approximating a complex matrices scores with max-plus scores is that the max-plus scores can be computed very quickly. This approximation is typically accurate to within an order or magnitude and should be useful in practical problems where the true scores are known to vary widely.