Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Calum Hand
Bayesian Screening: Multi-test Bayesian Optimization Applied to in silico Material Screening
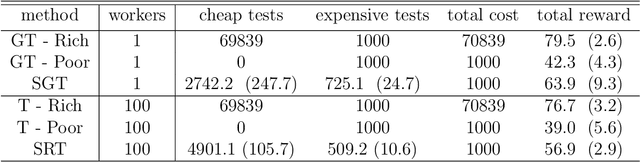
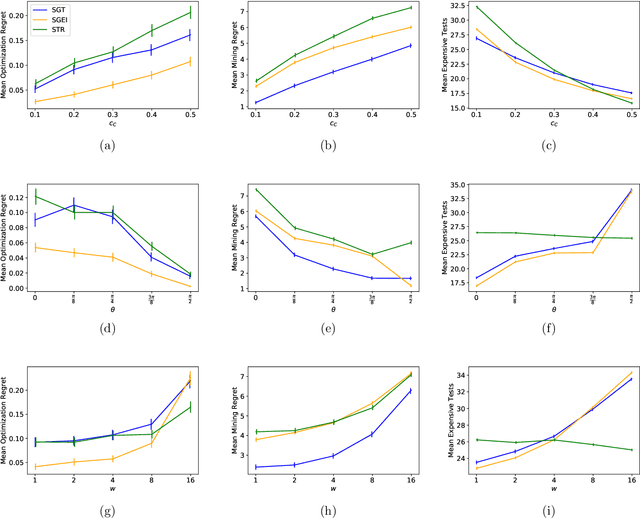
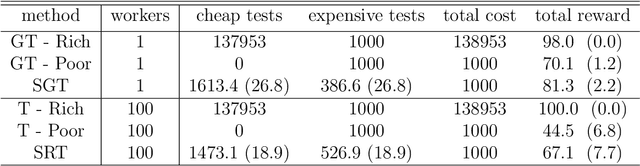
Sep 11, 2020Figures and Tables: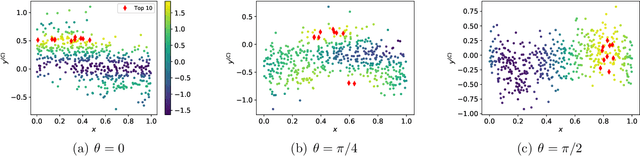




Abstract:We present new multi-test Bayesian optimization models and algorithms for use in large scale material screening applications. Our screening problems are designed around two tests, one expensive and one cheap. This paper differs from other recent work on multi-test Bayesian optimization through use of a flexible model that allows for complex, non-linear relationships between the cheap and expensive test scores. This additional modeling flexibility is essential in the material screening applications which we describe. We demonstrate the power of our new algorithms on a family of synthetic toy problems as well as on real data from two large scale screening studies.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge