Latitude: A Model for Mixed Linear-Tropical Matrix Factorization

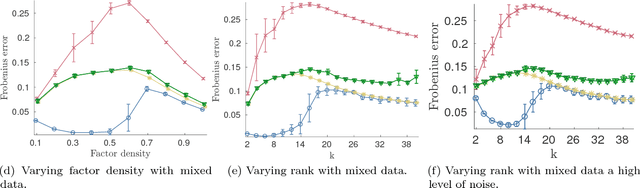
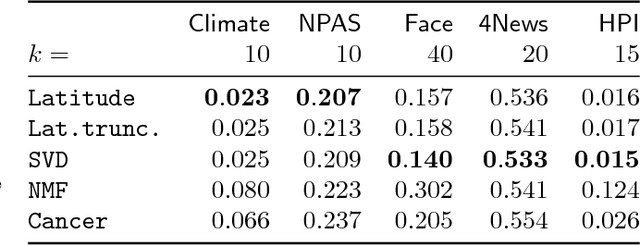
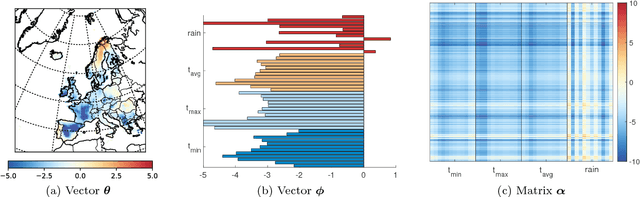
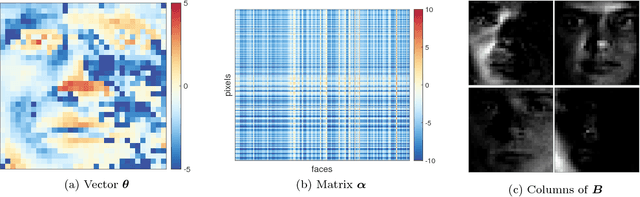
Nonnegative matrix factorization (NMF) is one of the most frequently-used matrix factorization models in data analysis. A significant reason to the popularity of NMF is its interpretability and the `parts of whole' interpretation of its components. Recently, max-times, or subtropical, matrix factorization (SMF) has been introduced as an alternative model with equally interpretable `winner takes it all' interpretation. In this paper we propose a new mixed linear--tropical model, and a new algorithm, called Latitude, that combines NMF and SMF, being able to smoothly alternate between the two. In our model, the data is modeled using the latent factors and latent parameters that control whether the factors are interpreted as NMF or SMF features, or their mixtures. We present an algorithm for our novel matrix factorization. Our experiments show that our algorithm improves over both baselines, and can yield interpretable results that reveal more of the latent structure than either NMF or SMF alone.

Algorithms for Approximate Subtropical Matrix Factorization

Matrix factorization methods are important tools in data mining and analysis. They can be used for many tasks, ranging from dimensionality reduction to visualization. In this paper we concentrate on the use of matrix factorizations for finding patterns from the data. Rather than using the standard algebra -- and the summation of the rank-1 components to build the approximation of the original matrix -- we use the subtropical algebra, which is an algebra over the nonnegative real values with the summation replaced by the maximum operator. Subtropical matrix factorizations allow "winner-takes-it-all" interpretations of the rank-1 components, revealing different structure than the normal (nonnegative) factorizations. We study the complexity and sparsity of the factorizations, and present a framework for finding low-rank subtropical factorizations. We present two specific algorithms, called Capricorn and Cancer, that are part of our framework. They can be used with data that has been corrupted with different types of noise, and with different error metrics, including the sum-of-absolute differences, Frobenius norm, and Jensen--Shannon divergence. Our experiments show that the algorithms perform well on data that has subtropical structure, and that they can find factorizations that are both sparse and easy to interpret.