On the connection between Noise-Contrastive Estimation and Contrastive Divergence

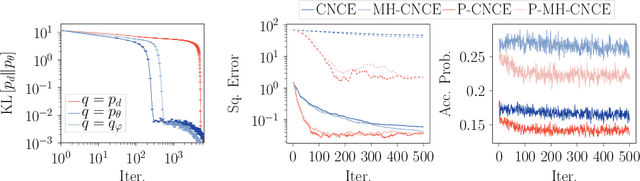
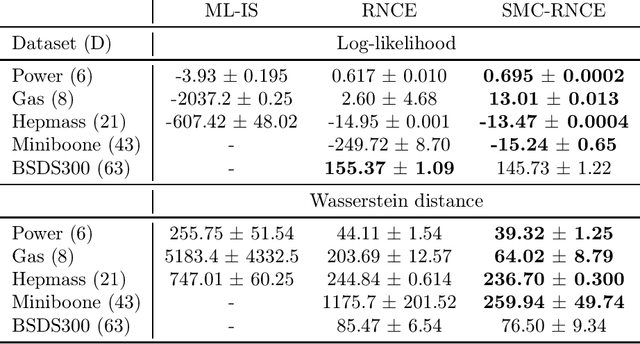
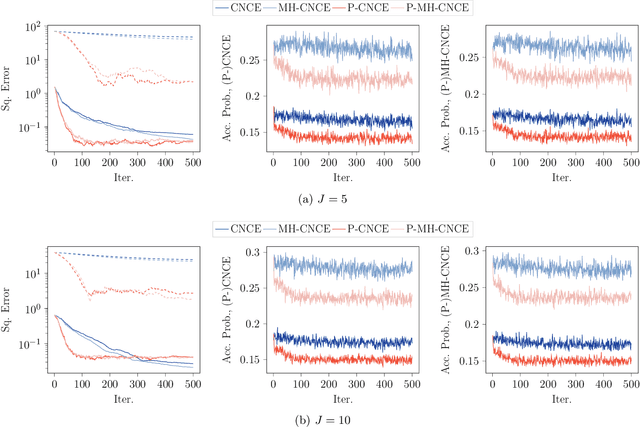
Noise-contrastive estimation (NCE) is a popular method for estimating unnormalised probabilistic models, such as energy-based models, which are effective for modelling complex data distributions. Unlike classical maximum likelihood (ML) estimation that relies on importance sampling (resulting in ML-IS) or MCMC (resulting in contrastive divergence, CD), NCE uses a proxy criterion to avoid the need for evaluating an often intractable normalisation constant. Despite apparent conceptual differences, we show that two NCE criteria, ranking NCE (RNCE) and conditional NCE (CNCE), can be viewed as ML estimation methods. Specifically, RNCE is equivalent to ML estimation combined with conditional importance sampling, and both RNCE and CNCE are special cases of CD. These findings bridge the gap between the two method classes and allow us to apply techniques from the ML-IS and CD literature to NCE, offering several advantageous extensions.

MCMC-Correction of Score-Based Diffusion Models for Model Composition

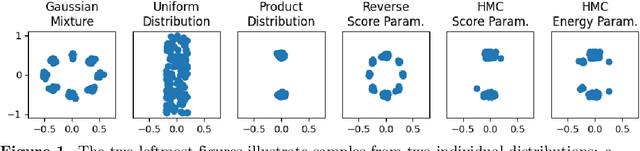
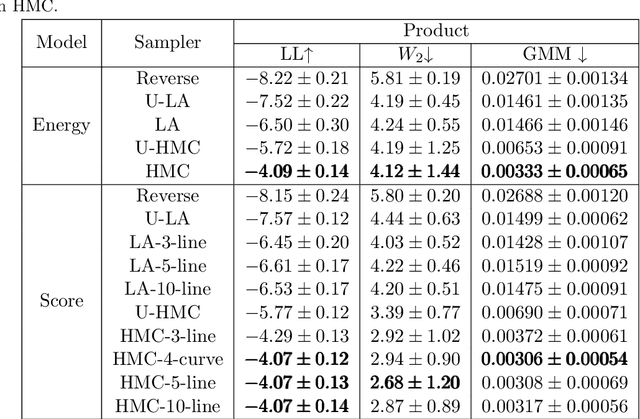
Diffusion models can be parameterised in terms of either a score or an energy function. The energy parameterisation has better theoretical properties, mainly that it enables an extended sampling procedure with a Metropolis--Hastings correction step, based on the change in total energy in the proposed samples. However, it seems to yield slightly worse performance, and more importantly, due to the widespread popularity of score-based diffusion, there are limited availability of off-the-shelf pre-trained energy-based ones. This limitation undermines the purpose of model composition, which aims to combine pre-trained models to sample from new distributions. Our proposal, however, suggests retaining the score parameterization and instead computing the energy-based acceptance probability through line integration of the score function. This allows us to re-use existing diffusion models and still combine the reverse process with various Markov-Chain Monte Carlo (MCMC) methods. We evaluate our method on a 2D experiment and find that it achieve similar or arguably better performance than the energy parameterisation.

Active Learning with Weak Labels for Gaussian Processes

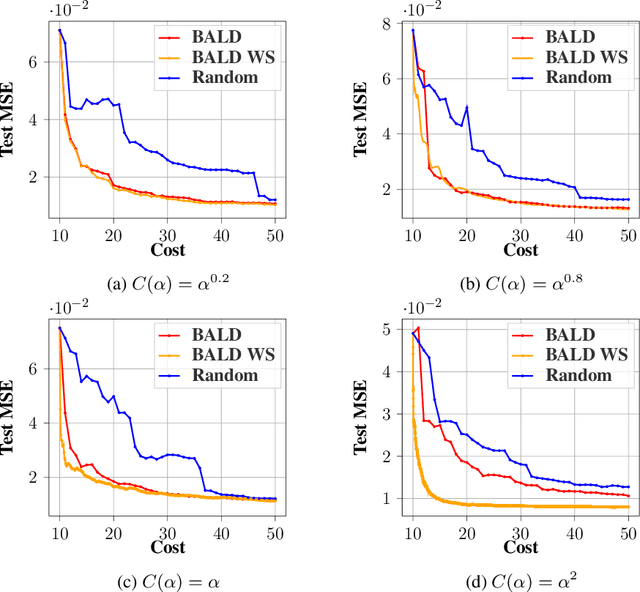
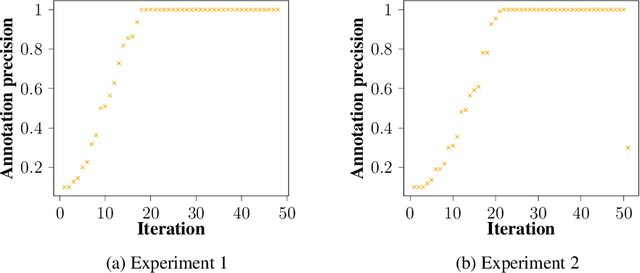
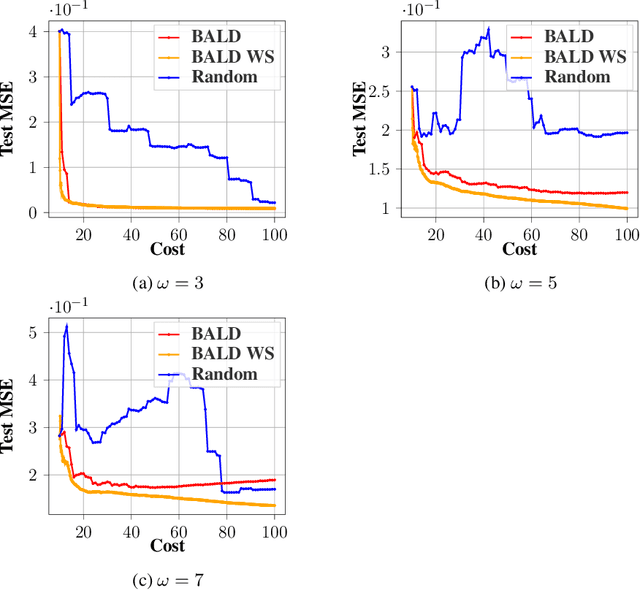
Annotating data for supervised learning can be costly. When the annotation budget is limited, active learning can be used to select and annotate those observations that are likely to give the most gain in model performance. We propose an active learning algorithm that, in addition to selecting which observation to annotate, selects the precision of the annotation that is acquired. Assuming that annotations with low precision are cheaper to obtain, this allows the model to explore a larger part of the input space, with the same annotation costs. We build our acquisition function on the previously proposed BALD objective for Gaussian Processes, and empirically demonstrate the gains of being able to adjust the annotation precision in the active learning loop.

A general framework for ensemble distribution distillation

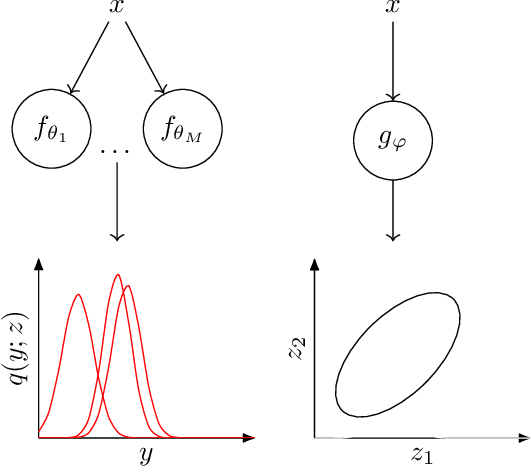
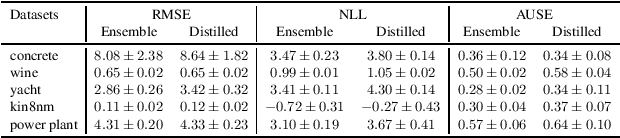
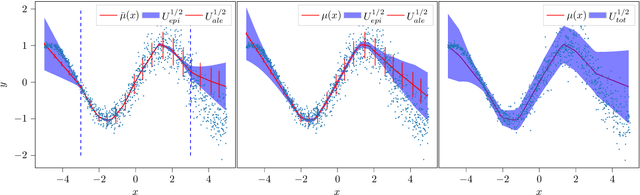
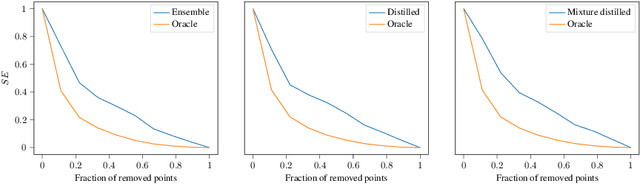
Ensembles of neural networks have been shown to give better performance than single networks, both in terms of predictions and uncertainty estimation. Additionally, ensembles allow the uncertainty to be decomposed into aleatoric (data) and epistemic (model) components, giving a more complete picture of the predictive uncertainty. Ensemble distillation is the process of compressing an ensemble into a single model, often resulting in a leaner model that still outperforms the individual ensemble members. Unfortunately, standard distillation erases the natural uncertainty decomposition of the ensemble. We present a general framework for distilling both regression and classification ensembles in a way that preserves the decomposition. We demonstrate the desired behaviour of our framework and show that its predictive performance is on par with standard distillation.