Towards understanding epoch-wise double descent in two-layer linear neural networks

Epoch-wise double descent is the phenomenon where generalisation performance improves beyond the point of overfitting, resulting in a generalisation curve exhibiting two descents under the course of learning. Understanding the mechanisms driving this behaviour is crucial not only for understanding the generalisation behaviour of machine learning models in general, but also for employing conventional selection methods, such as the use of early stopping to mitigate overfitting. While we ultimately want to draw conclusions of more complex models, such as deep neural networks, a majority of theoretical conclusions regarding the underlying cause of epoch-wise double descent are based on simple models, such as standard linear regression. To start bridging this gap, we study epoch-wise double descent in two-layer linear neural networks. First, we derive a gradient flow for the linear two-layer model, that bridges the learning dynamics of the standard linear regression model, and the linear two-layer diagonal network with quadratic weights. Second, we identify additional factors of epoch-wise double descent emerging with the extra model layer, by deriving necessary conditions for the generalisation error to follow a double descent pattern. While epoch-wise double descent in linear regression has been attributed to differences in input variance, in the two-layer model, also the singular values of the input-output covariance matrix play an important role. This opens up for further questions regarding unidentified factors of epoch-wise double descent for truly deep models.

On the connection between Noise-Contrastive Estimation and Contrastive Divergence

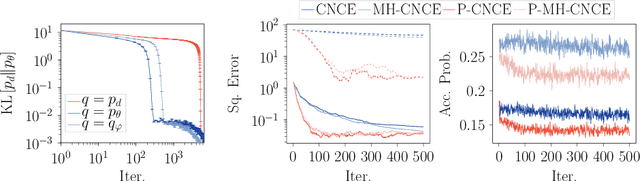
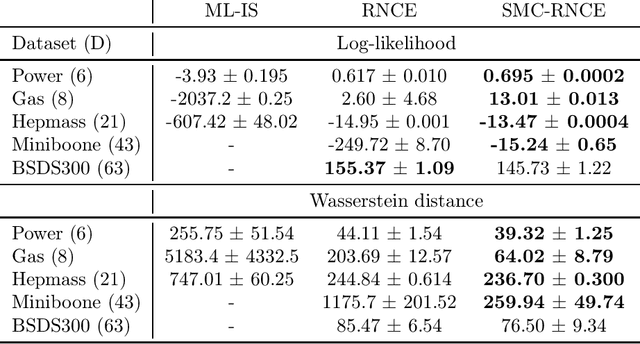
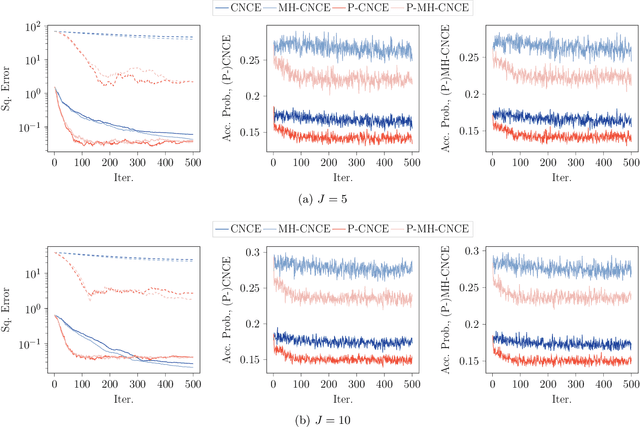
Noise-contrastive estimation (NCE) is a popular method for estimating unnormalised probabilistic models, such as energy-based models, which are effective for modelling complex data distributions. Unlike classical maximum likelihood (ML) estimation that relies on importance sampling (resulting in ML-IS) or MCMC (resulting in contrastive divergence, CD), NCE uses a proxy criterion to avoid the need for evaluating an often intractable normalisation constant. Despite apparent conceptual differences, we show that two NCE criteria, ranking NCE (RNCE) and conditional NCE (CNCE), can be viewed as ML estimation methods. Specifically, RNCE is equivalent to ML estimation combined with conditional importance sampling, and both RNCE and CNCE are special cases of CD. These findings bridge the gap between the two method classes and allow us to apply techniques from the ML-IS and CD literature to NCE, offering several advantageous extensions.

Active Learning with Weak Labels for Gaussian Processes

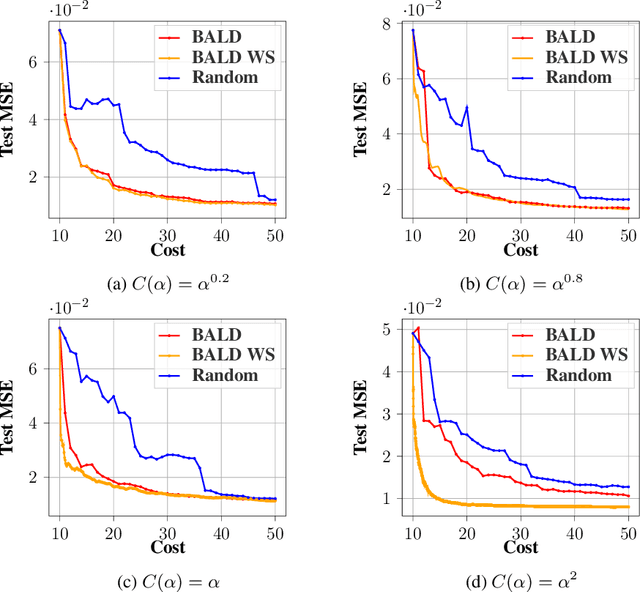
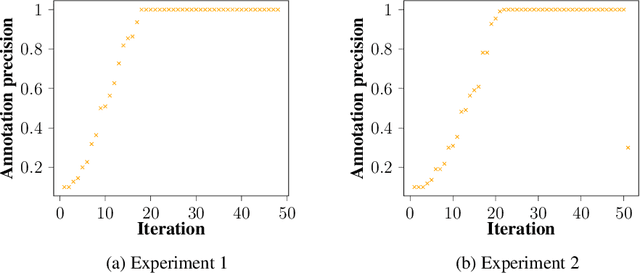
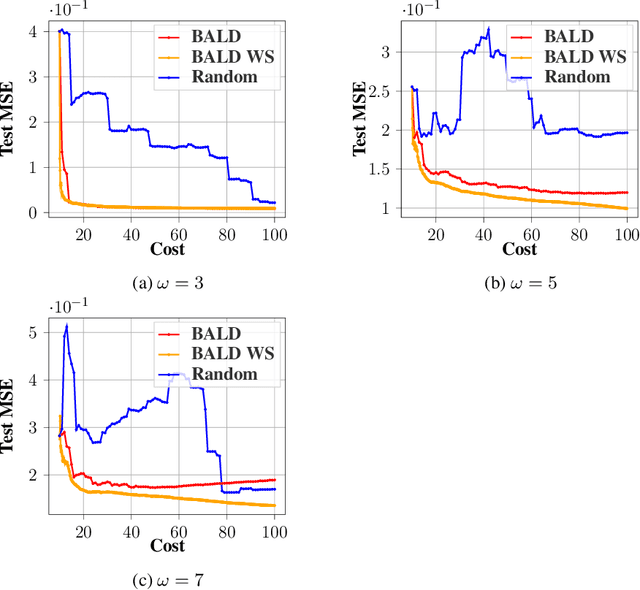
Annotating data for supervised learning can be costly. When the annotation budget is limited, active learning can be used to select and annotate those observations that are likely to give the most gain in model performance. We propose an active learning algorithm that, in addition to selecting which observation to annotate, selects the precision of the annotation that is acquired. Assuming that annotations with low precision are cheaper to obtain, this allows the model to explore a larger part of the input space, with the same annotation costs. We build our acquisition function on the previously proposed BALD objective for Gaussian Processes, and empirically demonstrate the gains of being able to adjust the annotation precision in the active learning loop.

Robustness and reliability when training with noisy labels

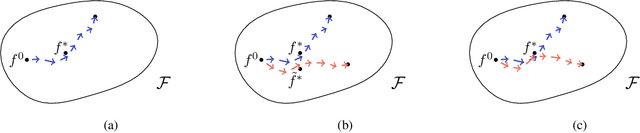
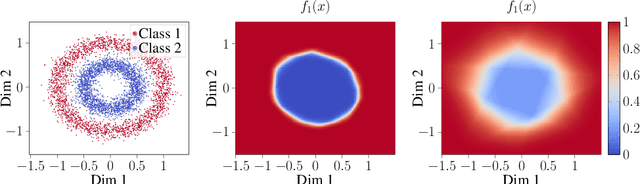
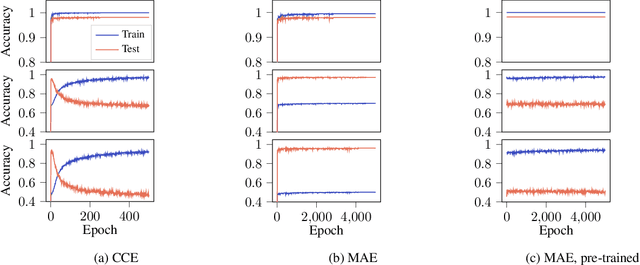
Labelling of data for supervised learning can be costly and time-consuming and the risk of incorporating label noise in large data sets is imminent. If training a flexible discriminative model using a strictly proper loss, such noise will inevitably shift the solution towards the conditional distribution over noisy labels. Nevertheless, while deep neural networks have proved capable of fitting random labels, regularisation and the use of robust loss functions empirically mitigate the effects of label noise. However, such observations concern robustness in accuracy, which is insufficient if reliable uncertainty quantification is critical. We demonstrate this by analysing the properties of the conditional distribution over noisy labels for an input-dependent noise model. In addition, we evaluate the set of robust loss functions characterised by an overlap in asymptotic risk minimisers under the clean and noisy data distributions. We find that strictly proper and robust loss functions both offer asymptotic robustness in accuracy, but neither guarantee that the resulting model is calibrated. Moreover, overfitting is an issue in practice. With these results, we aim to explain inherent robustness of algorithms to label noise and to give guidance in the development of new noise-robust algorithms.

A general framework for ensemble distribution distillation

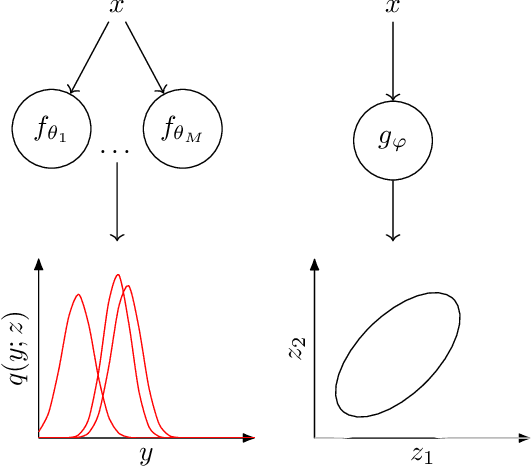
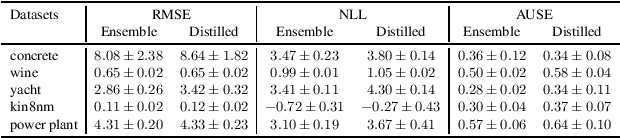
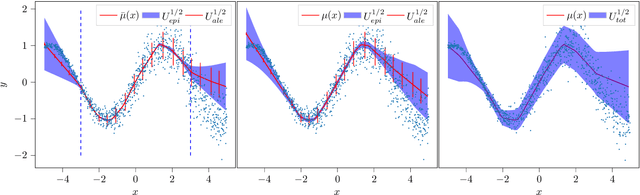
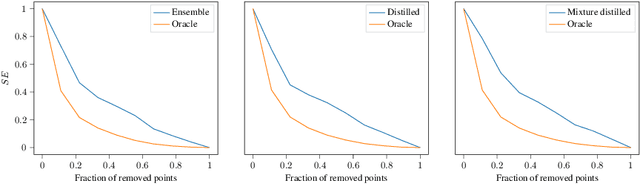
Ensembles of neural networks have been shown to give better performance than single networks, both in terms of predictions and uncertainty estimation. Additionally, ensembles allow the uncertainty to be decomposed into aleatoric (data) and epistemic (model) components, giving a more complete picture of the predictive uncertainty. Ensemble distillation is the process of compressing an ensemble into a single model, often resulting in a leaner model that still outperforms the individual ensemble members. Unfortunately, standard distillation erases the natural uncertainty decomposition of the ensemble. We present a general framework for distilling both regression and classification ensembles in a way that preserves the decomposition. We demonstrate the desired behaviour of our framework and show that its predictive performance is on par with standard distillation.