Nuclear Atomic Norm for parametric estimation of sparse channels

Parametric channel estimation in mmWave not only enables the anticipated large spectral efficiency gains of \acs{MIMO} systems but also reveals important propagation parameters, allowing for a low complexity representation of the channel matrix. In this work, we propose to use atomic norm as a gridless multidimensional spectral estimation approach to address parametric channel estimation where both AoD and AoA are identified. The conditions for recovery of the propagation parameters are given depending on properties of the measurement matrix, and on structural features such as the antenna geometry or the number of scatters to resolve. The proposed methodology is compared against several state-of-the-art parametric approaches.

Rényi Entropy Bounds on the Active Learning Cost-Performance Tradeoff

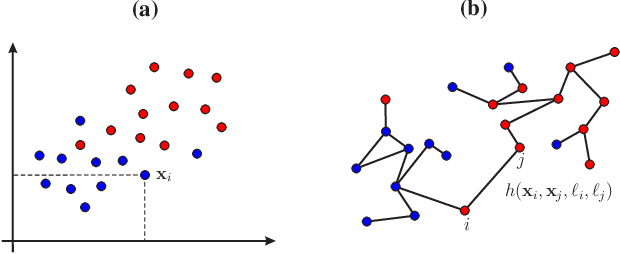
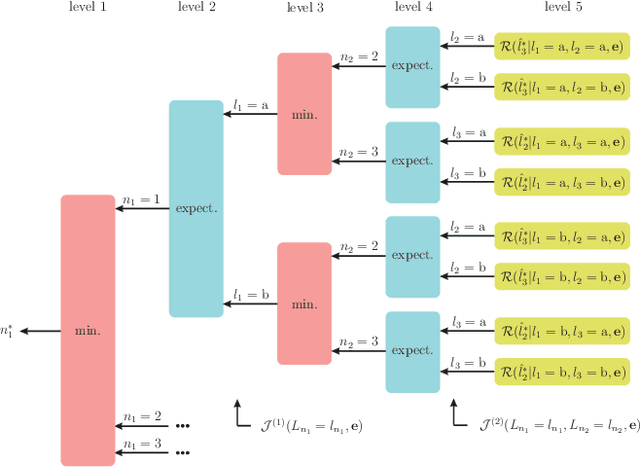
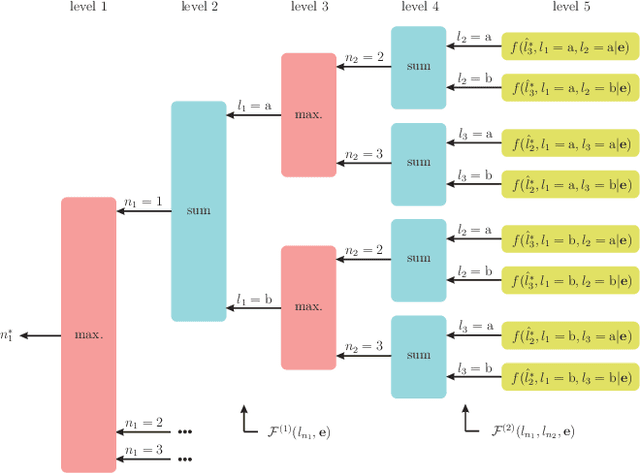
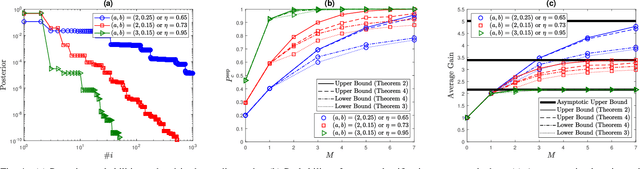
Semi-supervised classification, one of the most prominent fields in machine learning, studies how to combine the statistical knowledge of the often abundant unlabeled data with the often limited labeled data in order to maximize overall classification accuracy. In this context, the process of actively choosing the data to be labeled is referred to as active learning. In this paper, we initiate the non-asymptotic analysis of the optimal policy for semi-supervised classification with actively obtained labeled data. Considering a general Bayesian classification model, we provide the first characterization of the jointly optimal active learning and semi-supervised classification policy, in terms of the cost-performance tradeoff driven by the label query budget (number of data items to be labeled) and overall classification accuracy. Leveraging recent results on the R\'enyi Entropy, we derive tight information-theoretic bounds on such active learning cost-performance tradeoff.

Active learning in the geometric block model

The geometric block model is a recently proposed generative model for random graphs that is able to capture the inherent geometric properties of many community detection problems, providing more accurate characterizations of practical community structures compared with the popular stochastic block model. Galhotra et al. recently proposed a motif-counting algorithm for unsupervised community detection in the geometric block model that is proved to be near-optimal. They also characterized the regimes of the model parameters for which the proposed algorithm can achieve exact recovery. In this work, we initiate the study of active learning in the geometric block model. That is, we are interested in the problem of exactly recovering the community structure of random graphs following the geometric block model under arbitrary model parameters, by possibly querying the labels of a limited number of chosen nodes. We propose two active learning algorithms that combine the idea of motif-counting with two different label query policies. Our main contribution is to show that sampling the labels of a vanishingly small fraction of nodes (sub-linear in the total number of nodes) is sufficient to achieve exact recovery in the regimes under which the state-of-the-art unsupervised method fails. We validate the superior performance of our algorithms via numerical simulations on both real and synthetic datasets.