Rényi Entropy Bounds on the Active Learning Cost-Performance Tradeoff
Paper and Code
Feb 05, 2020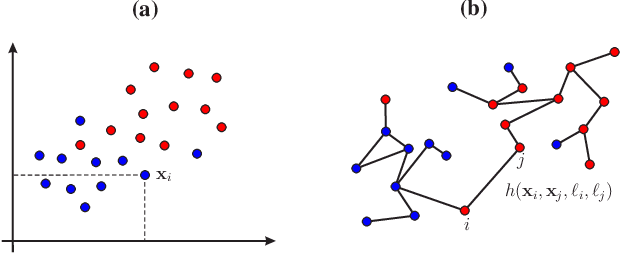
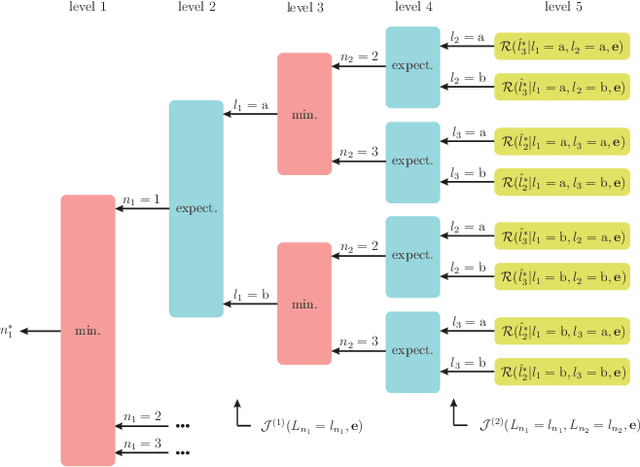
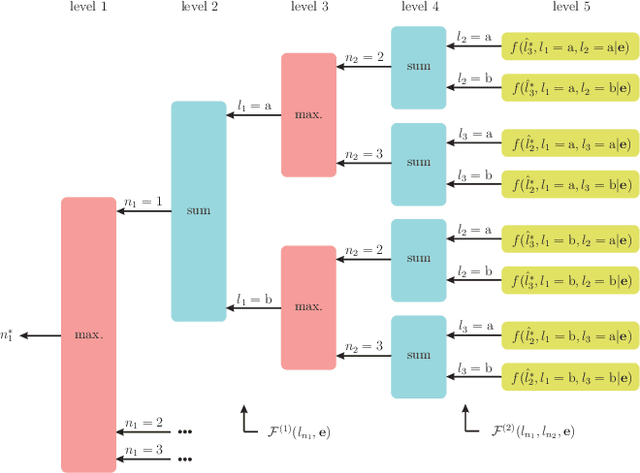
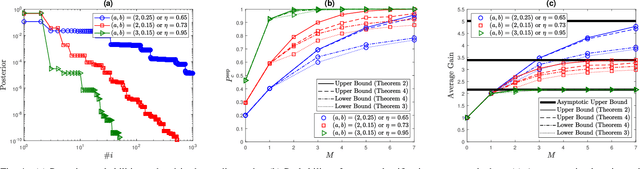
Semi-supervised classification, one of the most prominent fields in machine learning, studies how to combine the statistical knowledge of the often abundant unlabeled data with the often limited labeled data in order to maximize overall classification accuracy. In this context, the process of actively choosing the data to be labeled is referred to as active learning. In this paper, we initiate the non-asymptotic analysis of the optimal policy for semi-supervised classification with actively obtained labeled data. Considering a general Bayesian classification model, we provide the first characterization of the jointly optimal active learning and semi-supervised classification policy, in terms of the cost-performance tradeoff driven by the label query budget (number of data items to be labeled) and overall classification accuracy. Leveraging recent results on the R\'enyi Entropy, we derive tight information-theoretic bounds on such active learning cost-performance tradeoff.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge