Class-wise Autoencoders Measure Classification Difficulty And Detect Label Mistakes

We introduce a new framework for analyzing classification datasets based on the ratios of reconstruction errors between autoencoders trained on individual classes. This analysis framework enables efficient characterization of datasets on the sample, class, and entire dataset levels. We define reconstruction error ratios (RERs) that probe classification difficulty and allow its decomposition into (1) finite sample size and (2) Bayes error and decision-boundary complexity. Through systematic study across 19 popular visual datasets, we find that our RER-based dataset difficulty probe strongly correlates with error rate for state-of-the-art (SOTA) classification models. By interpreting sample-level classification difficulty as a label mistakenness score, we further find that RERs achieve SOTA performance on mislabel detection tasks on hard datasets under symmetric and asymmetric label noise. Our code is publicly available at https://github.com/voxel51/reconstruction-error-ratios.

Zero-Shot Coreset Selection: Efficient Pruning for Unlabeled Data

Deep learning increasingly relies on massive data with substantial costs for storage, annotation, and model training. To reduce these costs, coreset selection aims to find a representative subset of data to train models while ideally performing on par with the full data training. State-of-the-art coreset methods use carefully-designed criteria to quantify the importance of each data example via ground truth labels and dataset-specific training, then select examples whose scores lie in a certain range to construct a coreset. These methods work well in their respective settings, however, they cannot select data that are unlabeled, which is the majority of real-world data. To that end, this paper motivates and formalizes the problem of unlabeled coreset selection to enable greater scale and reduce annotation costs for deep learning. As a solution, we develop Zero-Shot Coreset Selection (ZCore), a method that efficiently selects coresets without ground truth labels or training on candidate data. Instead, ZCore uses existing foundation models to generate a zero-shot embedding space for unlabeled data, then quantifies the relative importance of each example based on overall coverage and redundancy within the embedding distribution. We evaluate ZCore on four datasets and outperform several state-of-the-art label-based methods, leading to a strong baseline for future research in unlabeled coreset selection. On ImageNet, ZCore selections achieve a downstream model accuracy of 53.99% with only 10% training data, which outperforms label-based methods while removing annotation requirements for 1.15 million images. Our code is publicly available at https://github.com/voxel51/zcore.

Quantum Hamiltonian-Based Models and the Variational Quantum Thermalizer Algorithm

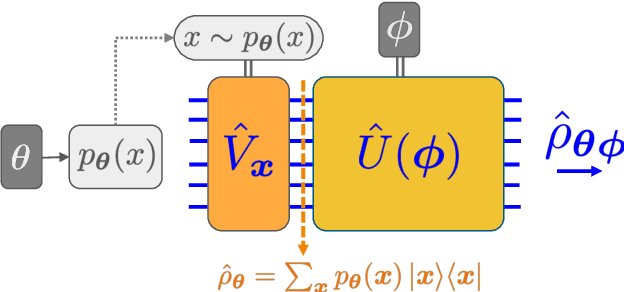
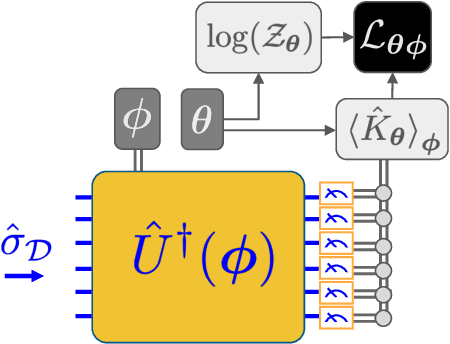
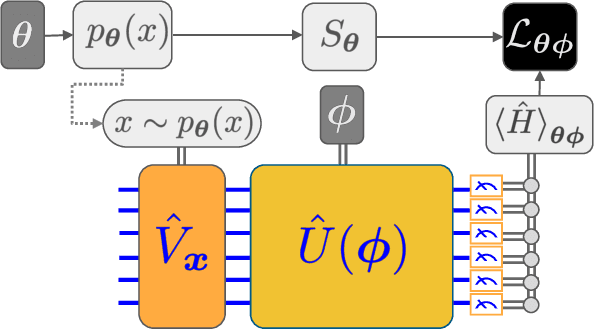
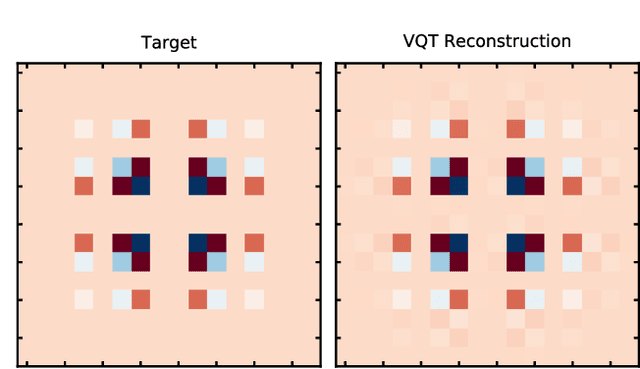
We introduce a new class of generative quantum-neural-network-based models called Quantum Hamiltonian-Based Models (QHBMs). In doing so, we establish a paradigmatic approach for quantum-probabilistic hybrid variational learning, where we efficiently decompose the tasks of learning classical and quantum correlations in a way which maximizes the utility of both classical and quantum processors. In addition, we introduce the Variational Quantum Thermalizer (VQT) for generating the thermal state of a given Hamiltonian and target temperature, a task for which QHBMs are naturally well-suited. The VQT can be seen as a generalization of the Variational Quantum Eigensolver (VQE) to thermal states: we show that the VQT converges to the VQE in the zero temperature limit. We provide numerical results demonstrating the efficacy of these techniques in illustrative examples. We use QHBMs and the VQT on Heisenberg spin systems, we apply QHBMs to learn entanglement Hamiltonians and compression codes in simulated free Bosonic systems, and finally we use the VQT to prepare thermal Fermionic Gaussian states for quantum simulation.