Bringing regularized optimal transport to lightspeed: a splitting method adapted for GPUs

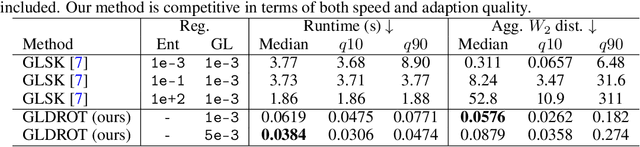
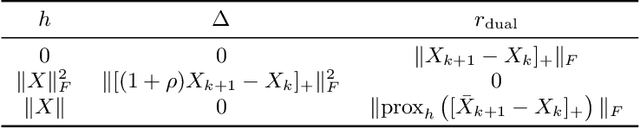
We present an efficient algorithm for regularized optimal transport. In contrast to previous methods, we use the Douglas-Rachford splitting technique to develop an efficient solver that can handle a broad class of regularizers. The algorithm has strong global convergence guarantees, low per-iteration cost, and can exploit GPU parallelization, making it considerably faster than the state-of-the-art for many problems. We illustrate its competitiveness in several applications, including domain adaptation and learning of generative models.

A Fast and Accurate Splitting Method for Optimal Transport: Analysis and Implementation

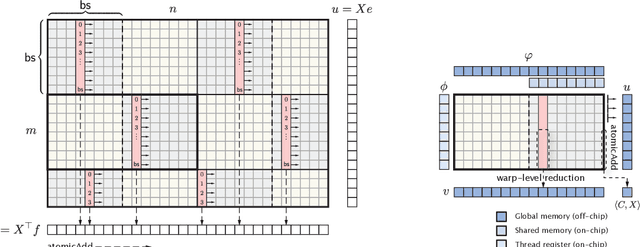
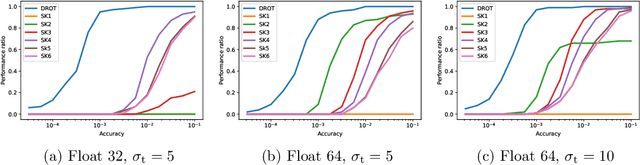
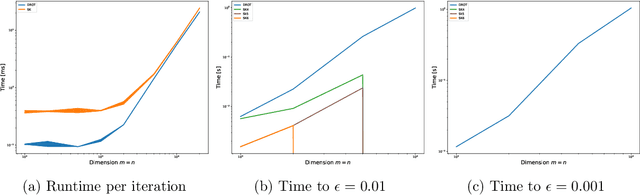
We develop a fast and reliable method for solving large-scale optimal transport (OT) problems at an unprecedented combination of speed and accuracy. Built on the celebrated Douglas-Rachford splitting technique, our method tackles the original OT problem directly instead of solving an approximate regularized problem, as many state-of-the-art techniques do. This allows us to provide sparse transport plans and avoid numerical issues of methods that use entropic regularization. The algorithm has the same cost per iteration as the popular Sinkhorn method, and each iteration can be executed efficiently, in parallel. The proposed method enjoys an iteration complexity $O(1/\epsilon)$ compared to the best-known $O(1/\epsilon^2)$ of the Sinkhorn method. In addition, we establish a linear convergence rate for our formulation of the OT problem. We detail an efficient GPU implementation of the proposed method that maintains a primal-dual stopping criterion at no extra cost. Substantial experiments demonstrate the effectiveness of our method, both in terms of computation times and robustness.