A Fast and Accurate Splitting Method for Optimal Transport: Analysis and Implementation

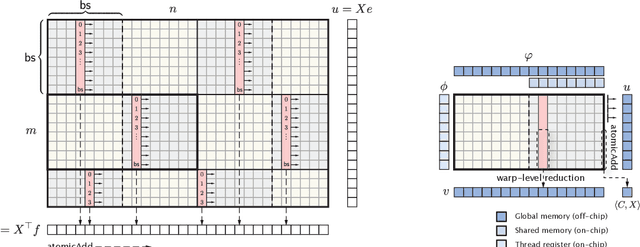
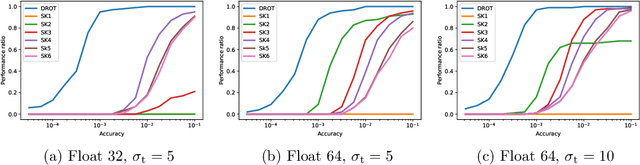
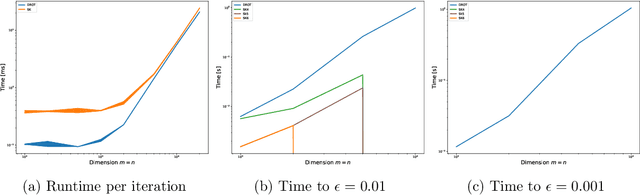
We develop a fast and reliable method for solving large-scale optimal transport (OT) problems at an unprecedented combination of speed and accuracy. Built on the celebrated Douglas-Rachford splitting technique, our method tackles the original OT problem directly instead of solving an approximate regularized problem, as many state-of-the-art techniques do. This allows us to provide sparse transport plans and avoid numerical issues of methods that use entropic regularization. The algorithm has the same cost per iteration as the popular Sinkhorn method, and each iteration can be executed efficiently, in parallel. The proposed method enjoys an iteration complexity $O(1/\epsilon)$ compared to the best-known $O(1/\epsilon^2)$ of the Sinkhorn method. In addition, we establish a linear convergence rate for our formulation of the OT problem. We detail an efficient GPU implementation of the proposed method that maintains a primal-dual stopping criterion at no extra cost. Substantial experiments demonstrate the effectiveness of our method, both in terms of computation times and robustness.

Stability and Convergence of Stochastic Gradient Clipping: Beyond Lipschitz Continuity and Smoothness

Stochastic gradient algorithms are often unstable when applied to functions that do not have Lipschitz-continuous and/or bounded gradients. Gradient clipping is a simple and effective technique to stabilize the training process for problems that are prone to the exploding gradient problem. Despite its widespread popularity, the convergence properties of the gradient clipping heuristic are poorly understood, especially for stochastic problems. This paper establishes both qualitative and quantitative convergence results of the clipped stochastic (sub)gradient method (SGD) for non-smooth convex functions with rapidly growing subgradients. Our analyses show that clipping enhances the stability of SGD and that the clipped SGD algorithm enjoys finite convergence rates in many cases. We also study the convergence of a clipped method with momentum, which includes clipped SGD as a special case, for weakly convex problems under standard assumptions. With a novel Lyapunov analysis, we show that the proposed method achieves the best-known rate for the considered class of problems, demonstrating the effectiveness of clipped methods also in this regime. Numerical results confirm our theoretical developments.

Convergence of a Stochastic Gradient Method with Momentum for Nonsmooth Nonconvex Optimization

Stochastic gradient methods with momentum are widely used in applications and at the core of optimization subroutines in many popular machine learning libraries. However, their sample complexities have never been obtained for problems that are non-convex and non-smooth. This paper establishes the convergence rate of a stochastic subgradient method with a momentum term of Polyak type for a broad class of non-smooth, non-convex, and constrained optimization problems. Our key innovation is the construction of a special Lyapunov function for which the proven complexity can be achieved without any tunning of the momentum parameter. For smooth problems, we extend the known complexity bound to the constrained case and demonstrate how the unconstrained case can be analyzed under weaker assumptions than the state-of-the-art. Numerical results confirm our theoretical developments.

Anderson Acceleration of Proximal Gradient Methods

Anderson acceleration is a well-established and simple technique for speeding up fixed-point computations with countless applications. Previous studies of Anderson acceleration in optimization have only been able to provide convergence guarantees for unconstrained and smooth problems. This work introduces novel methods for adapting Anderson acceleration to (non-smooth and constrained) proximal gradient algorithms. Under some technical conditions, we extend the existing local convergence results of Anderson acceleration for smooth fixed-point mappings to the proposed scheme. We also prove analytically that it is not, in general, possible to guarantee global convergence of native Anderson acceleration. We therefore propose a simple scheme for stabilization that combines the global worst-case guarantees of proximal gradient methods with the local adaptation and practical speed-up of Anderson acceleration.

Noisy Accelerated Power Method for Eigenproblems with Applications

This paper introduces an efficient algorithm for finding the dominant generalized eigenvectors of a pair of symmetric matrices. Combining tools from approximation theory and convex optimization, we develop a simple scalable algorithm with strong theoretical performance guarantees. More precisely, the algorithm retains the simplicity of the well-known power method but enjoys the asymptotic iteration complexity of the powerful Lanczos method. Unlike these classic techniques, our algorithm is designed to decompose the overall problem into a series of subproblems that only need to be solved approximately. The combination of good initializations, fast iterative solvers, and appropriate error control in solving the subproblems lead to a linear running time in the input sizes compared to the superlinear time for the traditional methods. The improved running time immediately offers acceleration for several applications. As an example, we demonstrate how the proposed algorithm can be used to accelerate canonical correlation analysis, which is a fundamental statistical tool for learning of a low-dimensional representation of high-dimensional objects. Numerical experiments on real-world data sets confirm that our approach yields significant improvements over the current state-of-the-art.

Curvature-Exploiting Acceleration of Elastic Net Computations

This paper introduces an efficient second-order method for solving the elastic net problem. Its key innovation is a computationally efficient technique for injecting curvature information in the optimization process which admits a strong theoretical performance guarantee. In particular, we show improved run time over popular first-order methods and quantify the speed-up in terms of statistical measures of the data matrix. The improved time complexity is the result of an extensive exploitation of the problem structure and a careful combination of second-order information, variance reduction techniques, and momentum acceleration. Beside theoretical speed-up, experimental results demonstrate great practical performance benefits of curvature information, especially for ill-conditioned data sets.