Inertial Human Motion Capture: From Biomechanics to Recent Sensor Fusion Methods and Back

Inertial measurement units (IMUs) are a promising means to capture human motion, yet obtaining meaningful biomechanical quantities from IMU measurements remains non-trivial. This tutorial-style review focuses on kinematics and introduces four key aspects (inertial human motion capture objective, environmental conditions, subject & attributes, and motion characteristics) to determine how to translate biomechanical problems into adequate formulations for the fusion of inertial sensor measurements. We identify three fundamental challenges for kinematics estimation from IMUs: IMUs do not provide direct information about the joint angle, IMUs do not measure their own orientation, and real-world environments and dynamics compromise sensor reliability. Though there exist widely-used methods to overcome these challenges, they suffer from severe limitations in real-life applications, e.g., the need for sensor-to-segment calibration, and the fact that magnetic field disturbances degrade joint angle accuracy. The full potential for many use-cases hence remains untapped in terms of accuracy and reliability. We share insights into recently proposed methods, e.g. exploiting the human body's kinematic chain constraints, having the potential to overcome these limitations. We also present guiding questions related to the four key aspects and illustrate their use for navigating the methodological landscape for the use-case of lower-extremity joint angle estimation, for which we share open-access code and compare the traditional workflow with three alternatives. Our aim is to bridge the gap between the sensor fusion community developing methods for human motion capture and the biomechanics community in need of accurate, easy-to-use, and reliable methods to study human motion outside of the laboratory.

Dispelling Four Challenges in Inertial Motion Tracking with One Recurrent Inertial Graph-based Estimator (RING)

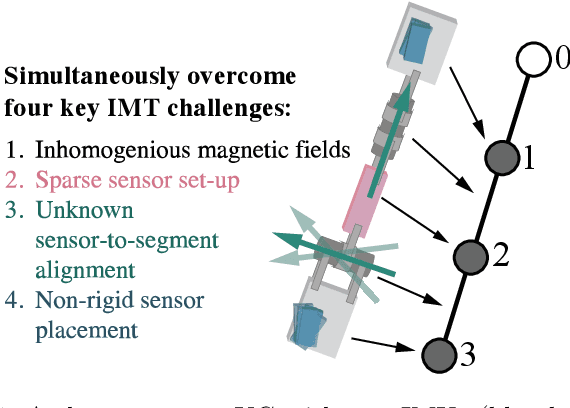
In this paper, we extend the Recurrent Inertial Graph-based Estimator (RING), a novel neural-network-based solution for Inertial Motion Tracking (IMT), to generalize across a large range of sampling rates, and we demonstrate that it can overcome four real-world challenges: inhomogeneous magnetic fields, sensor-to-segment misalignment, sparse sensor setups, and nonrigid sensor attachment. RING can estimate the rotational state of a three-segment kinematic chain with double hinge joints from inertial data, and achieves an experimental mean-absolute-(tracking)-error of 8.10 +/- 1.19 degrees if all four challenges are present simultaneously. The network is trained on simulated data yet evaluated on experimental data, highlighting its remarkable ability to zero-shot generalize from simulation to experiment. We conduct an ablation study to analyze the impact of each of the four challenges on RING's performance, we showcase its robustness to varying sampling rates, and we demonstrate that RING is capable of real-time operation. This research not only advances IMT technology by making it more accessible and versatile but also enhances its potential for new application domains including non-expert use of sparse IMT with nonrigid sensor attachments in unconstrained environments.

Observability of the relative motion from inertial data in kinematic chains

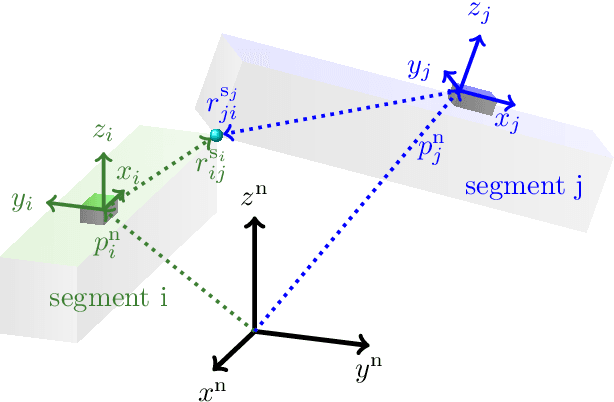
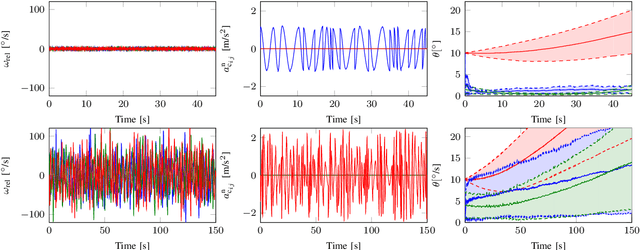
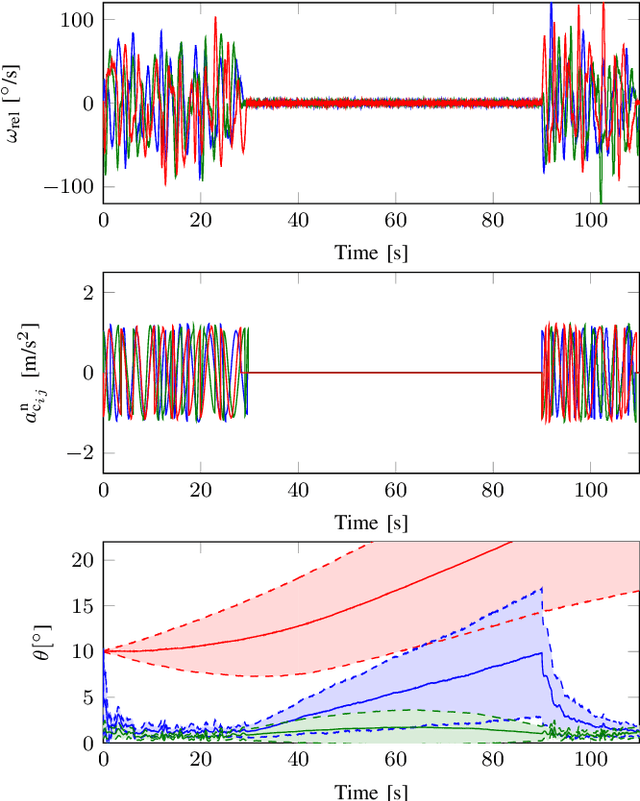
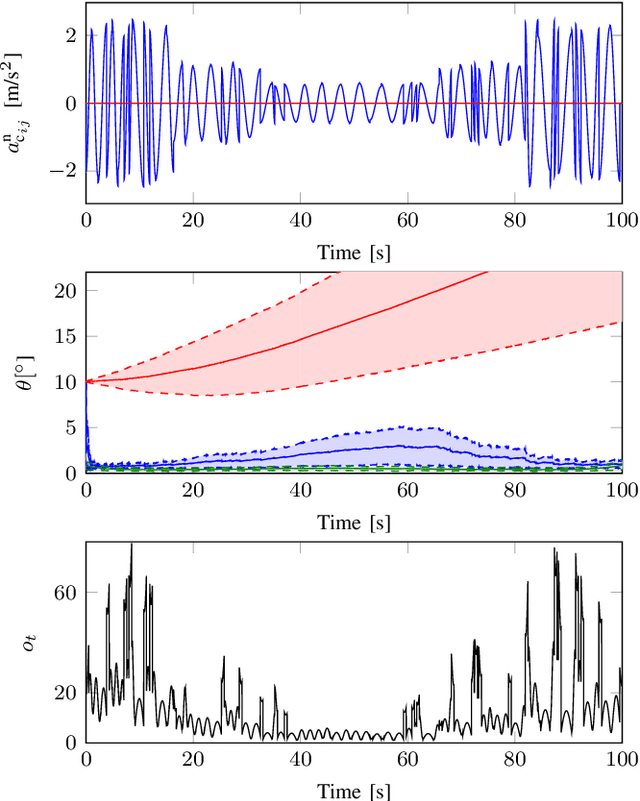
In recent years, it has been shown that the motion of kinematic chains can be estimated using measurements from inertial sensors placed on segments connected by rotational joints. These methods specifically avoid using magnetometer measurements, which are known to cause issues since the magnetic field at the different sensor locations is typically different. They rely on the assumption that the motion of the kinematic chain is sufficiently rich to assure / yield observability of the relative pose. However, a formal investigation of this crucial requirement has not yet been presented and no specific conditions for observability have so far been given. In this work, we present an observability analysis and show that the relative pose of the body segments is indeed observable under a very mild condition on the motion. We support these results by a simulation study, in which we also show the effect of stationary periods in the data and of the amount of excitation on the accuracy of the estimates. We use experimental data from a human gait experiment to show that the excitation level is sufficient for obtaining accurate estimates even when the subject remains stationary for a period of 47 seconds halfway during the experiment.