Ivan Markovic
GVDepth: Zero-Shot Monocular Depth Estimation for Ground Vehicles based on Probabilistic Cue Fusion
Dec 08, 2024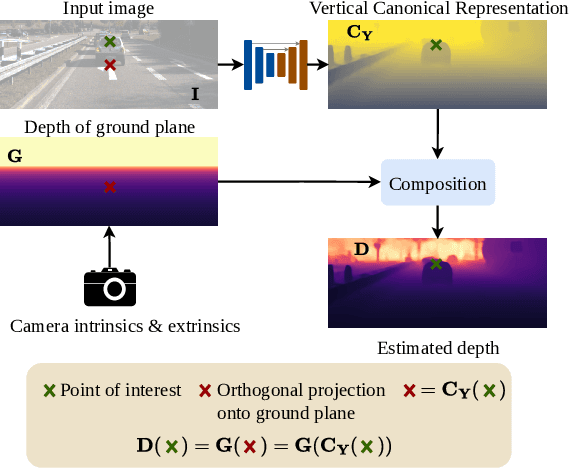
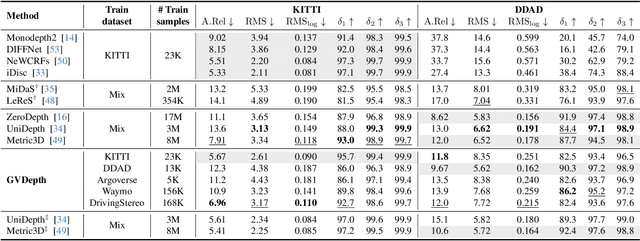
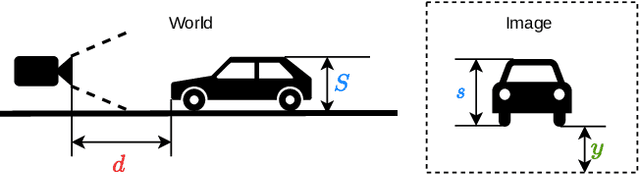
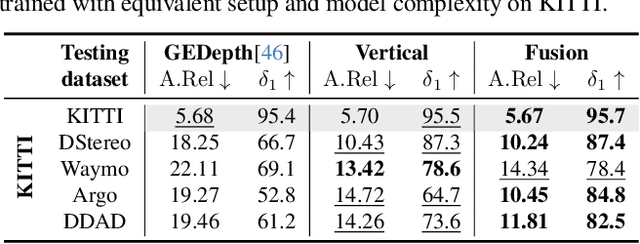
Abstract:Generalizing metric monocular depth estimation presents a significant challenge due to its ill-posed nature, while the entanglement between camera parameters and depth amplifies issues further, hindering multi-dataset training and zero-shot accuracy. This challenge is particularly evident in autonomous vehicles and mobile robotics, where data is collected with fixed camera setups, limiting the geometric diversity. Yet, this context also presents an opportunity: the fixed relationship between the camera and the ground plane imposes additional perspective geometry constraints, enabling depth regression via vertical image positions of objects. However, this cue is highly susceptible to overfitting, thus we propose a novel canonical representation that maintains consistency across varied camera setups, effectively disentangling depth from specific parameters and enhancing generalization across datasets. We also propose a novel architecture that adaptively and probabilistically fuses depths estimated via object size and vertical image position cues. A comprehensive evaluation demonstrates the effectiveness of the proposed approach on five autonomous driving datasets, achieving accurate metric depth estimation for varying resolutions, aspect ratios and camera setups. Notably, we achieve comparable accuracy to existing zero-shot methods, despite training on a single dataset with a single-camera setup.
Mixture Reduction on Matrix Lie Groups
Aug 18, 2017

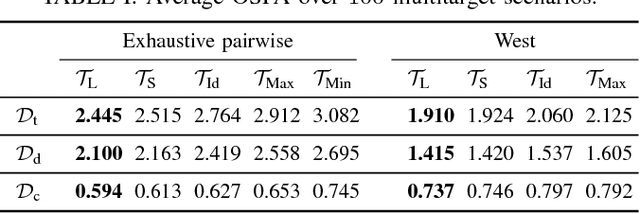
Abstract:Many physical systems evolve on matrix Lie groups and mixture filtering designed for such manifolds represent an inevitable tool for challenging estimation problems. However, mixture filtering faces the issue of a constantly growing number of components, hence require appropriate mixture reduction techniques. In this letter we propose a mixture reduction approach for distributions on matrix Lie groups, called the concentrated Gaussian distributions (CGDs). This entails appropriate reparametrization of CGD parameters to compute the KL divergence, pick and merge the mixture components. Furthermore, we also introduce a multitarget tracking filter on Lie groups as a mixture filtering study example for the proposed reduction method. In particular, we implemented the probability hypothesis density filter on matrix Lie groups. We validate the filter performance using the optimal subpattern assignment metric on a synthetic dataset consisting of 100 randomly generated multitarget scenarios.
On wrapping the Kalman filter and estimating with the SO group
Aug 18, 2017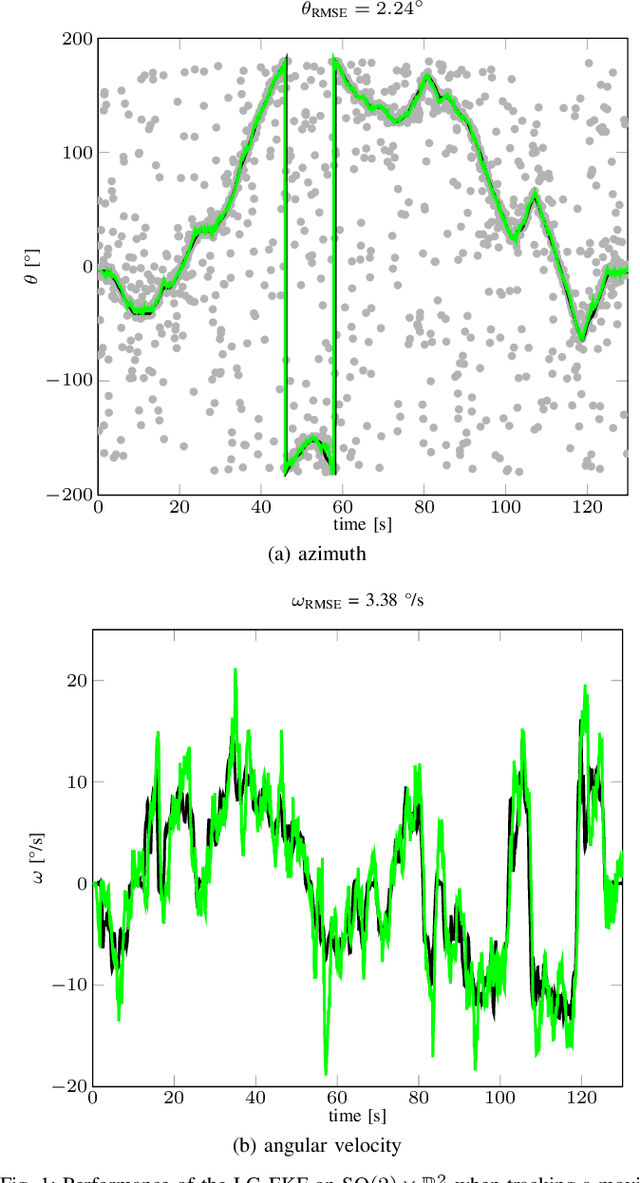
Abstract:This paper analyzes directional tracking in 2D with the extended Kalman filter on Lie groups (LG-EKF). The study stems from the problem of tracking objects moving in 2D Euclidean space, with the observer measuring direction only, thus rendering the measurement space and object position on the circle---a non-Euclidean geometry. The problem is further inconvenienced if we need to include higher-order dynamics in the state space, like angular velocity which is a Euclidean variables. The LG-EKF offers a solution to this issue by modeling the state space as a Lie group or combination thereof, e.g., SO(2) or its combinations with Rn. In the present paper, we first derive the LG-EKF on SO(2) and subsequently show that this derivation, based on the mathematically grounded framework of filtering on Lie groups, yields the same result as heuristically wrapping the angular variable within the EKF framework. This result applies only to the SO(2) and SO(2)xRn LG-EKFs and is not intended to be extended to other Lie groups or combinations thereof. In the end, we showcase the SO(2)xR2 LG-EKF, as an example of a constant angular acceleration model, on the problem of speaker tracking with a microphone array for which real-world experiments are conducted and accuracy is evaluated with ground truth data obtained by a motion capture system.
Moving object tracking employing rigid body motion on matrix Lie groups
Aug 18, 2017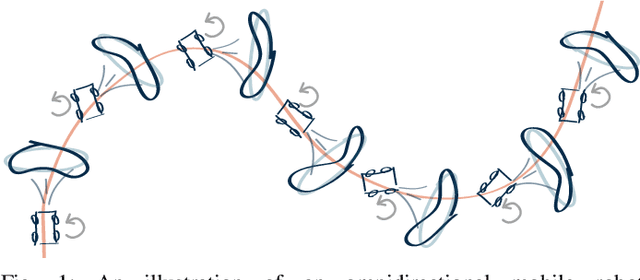
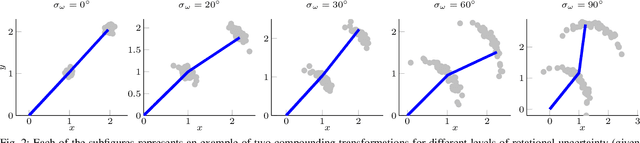
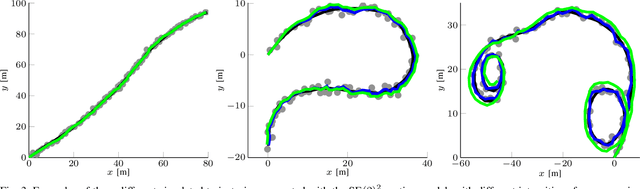
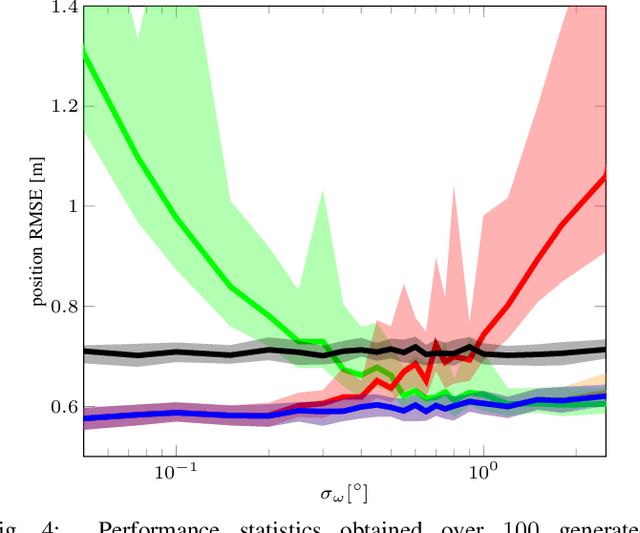
Abstract:In this paper we propose a novel method for estimating rigid body motion by modeling the object state directly in the space of the rigid body motion group SE(2). It has been recently observed that a noisy manoeuvring object in SE(2) exhibits banana-shaped probability density contours in its pose. For this reason, we propose and investigate two state space models for moving object tracking: (i) a direct product SE(2)xR3 and (ii) a direct product of the two rigid body motion groups SE(2)xSE(2). The first term within these two state space constructions describes the current pose of the rigid body, while the second one employs its second order dynamics, i.e., the velocities. By this, we gain the flexibility of tracking omnidirectional motion in the vein of a constant velocity model, but also accounting for the dynamics in the rotation component. Since the SE(2) group is a matrix Lie group, we solve this problem by using the extended Kalman filter on matrix Lie groups and provide a detailed derivation of the proposed filters. We analyze the performance of the filters on a large number of synthetic trajectories and compare them with (i) the extended Kalman filter based constant velocity and turn rate model and (ii) the linear Kalman filter based constant velocity model. The results show that the proposed filters outperform the other two filters on a wide spectrum of types of motion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge