Mixture Reduction on Matrix Lie Groups

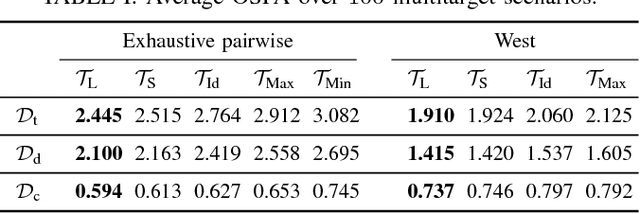
Many physical systems evolve on matrix Lie groups and mixture filtering designed for such manifolds represent an inevitable tool for challenging estimation problems. However, mixture filtering faces the issue of a constantly growing number of components, hence require appropriate mixture reduction techniques. In this letter we propose a mixture reduction approach for distributions on matrix Lie groups, called the concentrated Gaussian distributions (CGDs). This entails appropriate reparametrization of CGD parameters to compute the KL divergence, pick and merge the mixture components. Furthermore, we also introduce a multitarget tracking filter on Lie groups as a mixture filtering study example for the proposed reduction method. In particular, we implemented the probability hypothesis density filter on matrix Lie groups. We validate the filter performance using the optimal subpattern assignment metric on a synthetic dataset consisting of 100 randomly generated multitarget scenarios.