On wrapping the Kalman filter and estimating with the SO group

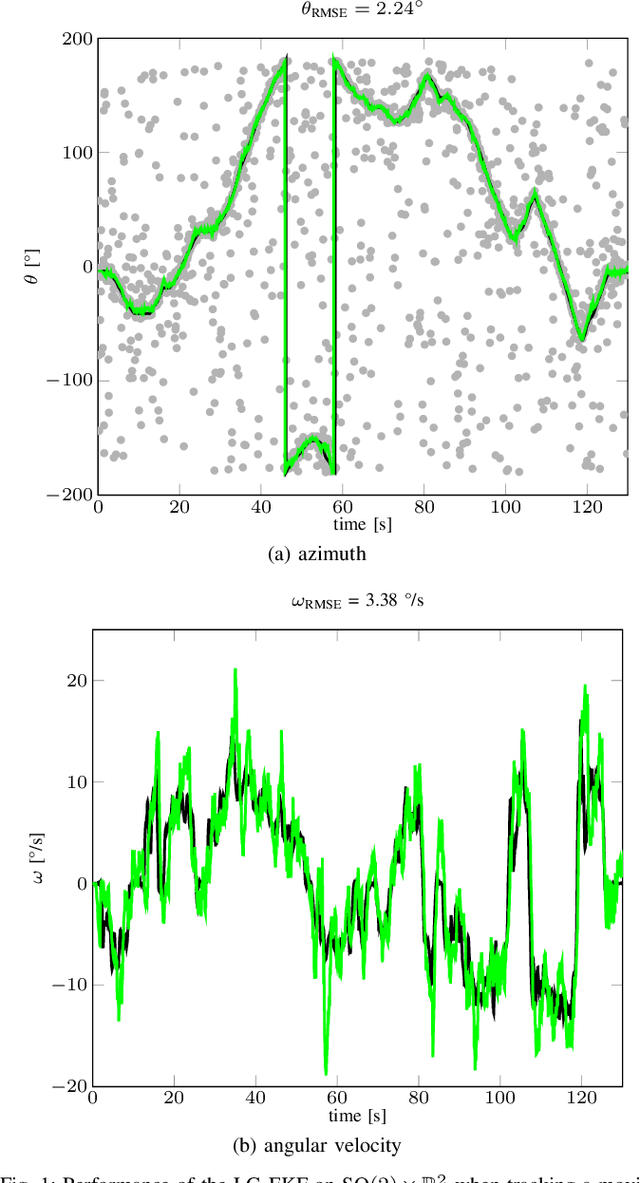
This paper analyzes directional tracking in 2D with the extended Kalman filter on Lie groups (LG-EKF). The study stems from the problem of tracking objects moving in 2D Euclidean space, with the observer measuring direction only, thus rendering the measurement space and object position on the circle---a non-Euclidean geometry. The problem is further inconvenienced if we need to include higher-order dynamics in the state space, like angular velocity which is a Euclidean variables. The LG-EKF offers a solution to this issue by modeling the state space as a Lie group or combination thereof, e.g., SO(2) or its combinations with Rn. In the present paper, we first derive the LG-EKF on SO(2) and subsequently show that this derivation, based on the mathematically grounded framework of filtering on Lie groups, yields the same result as heuristically wrapping the angular variable within the EKF framework. This result applies only to the SO(2) and SO(2)xRn LG-EKFs and is not intended to be extended to other Lie groups or combinations thereof. In the end, we showcase the SO(2)xR2 LG-EKF, as an example of a constant angular acceleration model, on the problem of speaker tracking with a microphone array for which real-world experiments are conducted and accuracy is evaluated with ground truth data obtained by a motion capture system.