Moving object tracking employing rigid body motion on matrix Lie groups
Paper and Code
Aug 18, 2017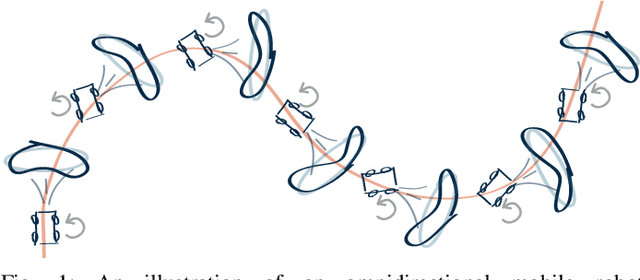
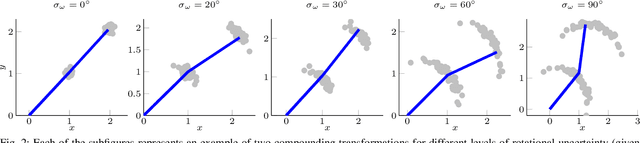
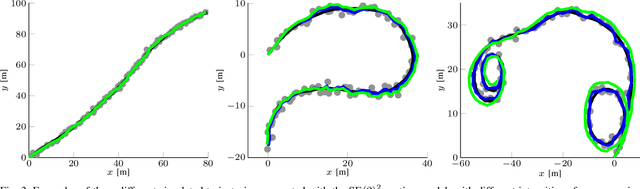
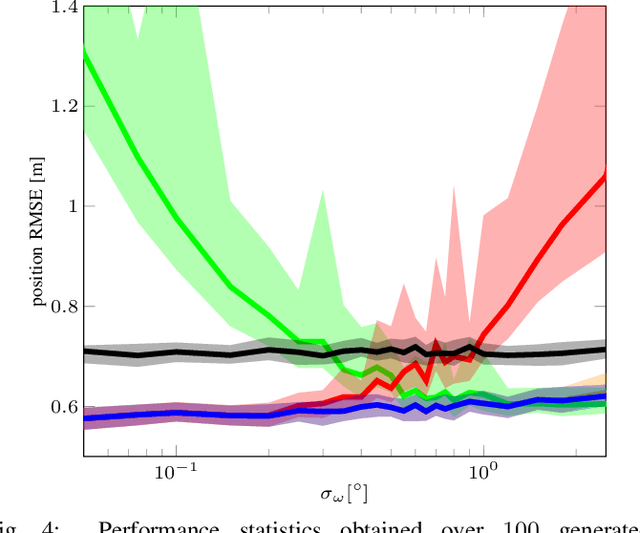
In this paper we propose a novel method for estimating rigid body motion by modeling the object state directly in the space of the rigid body motion group SE(2). It has been recently observed that a noisy manoeuvring object in SE(2) exhibits banana-shaped probability density contours in its pose. For this reason, we propose and investigate two state space models for moving object tracking: (i) a direct product SE(2)xR3 and (ii) a direct product of the two rigid body motion groups SE(2)xSE(2). The first term within these two state space constructions describes the current pose of the rigid body, while the second one employs its second order dynamics, i.e., the velocities. By this, we gain the flexibility of tracking omnidirectional motion in the vein of a constant velocity model, but also accounting for the dynamics in the rotation component. Since the SE(2) group is a matrix Lie group, we solve this problem by using the extended Kalman filter on matrix Lie groups and provide a detailed derivation of the proposed filters. We analyze the performance of the filters on a large number of synthetic trajectories and compare them with (i) the extended Kalman filter based constant velocity and turn rate model and (ii) the linear Kalman filter based constant velocity model. The results show that the proposed filters outperform the other two filters on a wide spectrum of types of motion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge