Ishaan Bassi
Detecting Anomaly in Chemical Sensors via L1-Kernels based Principal Component Analysis
Jan 07, 2022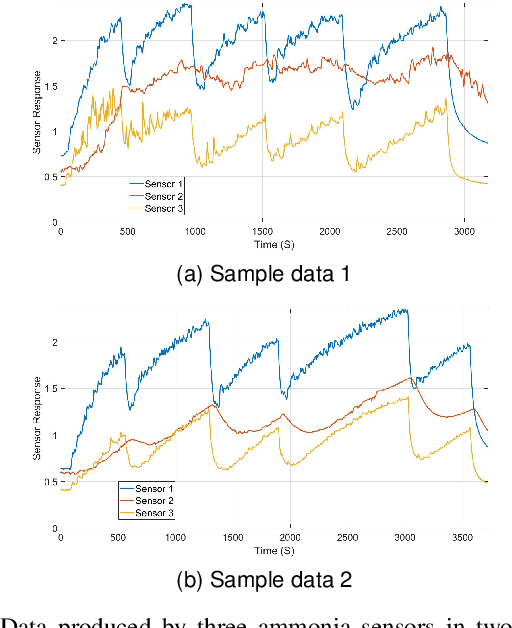
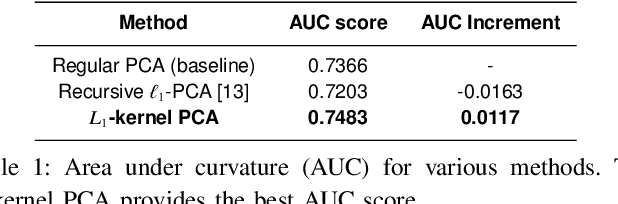
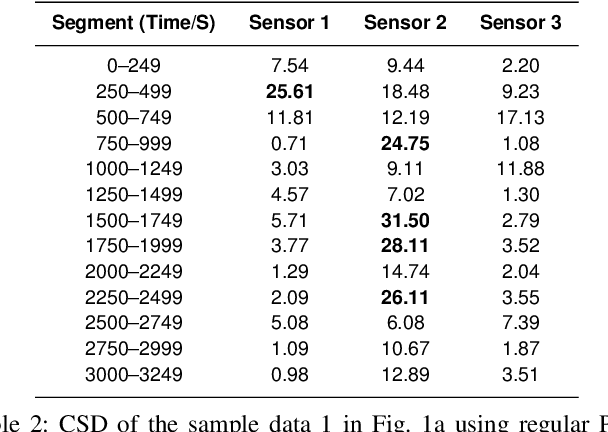
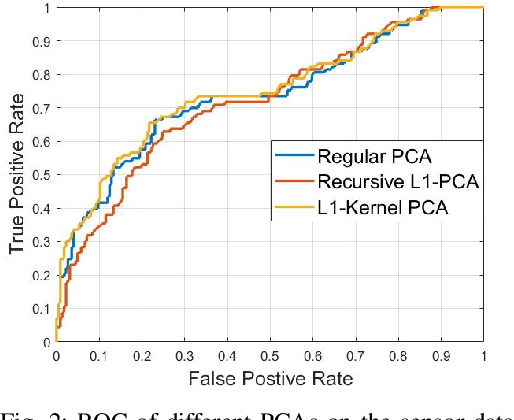
Abstract:We propose a kernel-PCA based method to detect anomaly in chemical sensors. We use temporal signals produced by chemical sensors to form vectors to perform the Principal Component Analysis (PCA). We estimate the kernel-covariance matrix of the sensor data and compute the eigenvector corresponding to the largest eigenvalue of the covariance matrix. The anomaly can be detected by comparing the difference between the actual sensor data and the reconstructed data from the dominant eigenvector. In this paper, we introduce a new multiplication-free kernel, which is related to the l1-norm for the anomaly detection task. The l1-kernel PCA is not only computationally efficient but also energy-efficient because it does not require any actual multiplications during the kernel covariance matrix computation. Our experimental results show that our kernel-PCA method achieves a higher area under curvature (AUC) score (0.7483) than the baseline regular PCA method (0.7366).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge