Non-congruent non-degenerate curves with identical signatures

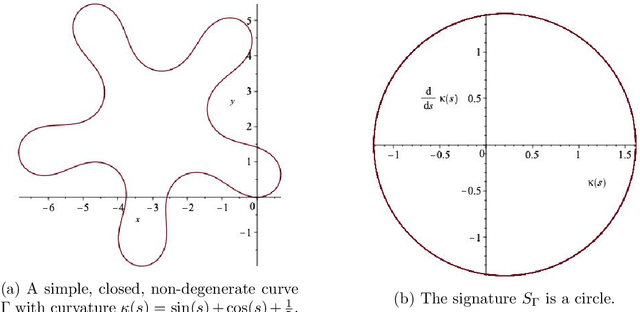
We construct examples of non-congruent, non-degenerate simple planar closed curves with identical Euclidean signatures, thus disproving a claim made in Hickman (J. Math Imaging Vis. 43:206-213, 2012) that all such curves must be congruent. Our examples include closed $C^\infty$ curves of the same length and the same symmetry group. We show a general mechanism for constructing such examples by exploiting the self-intersection points of the signature. We state an updated congruence criterion for simple closed non-degenerate curves and confirm that for curves with simple signatures the claim made by Hickman holds.

Invariants of objects and their images under surjective maps

We examine the relationships between the differential invariants of objects and of their images under a surjective map. We analyze both the case when the underlying transformation group is projectable and hence induces an action on the image, and the case when only a proper subgroup of the entire group acts projectably. In the former case, we establish a constructible isomorphism between the algebra of differential invariants of the images and the algebra of fiber-wise constant (gauge) differential invariants of the objects. In the latter case, we describe residual effects of the full transformation group on the image invariants. Our motivation comes from the problem of reconstruction of an object from multiple-view images, with central and parallel projections of curves from three-dimensional space to the two-dimensional plane serving as our main examples.

Object-image correspondence for curves under finite and affine cameras

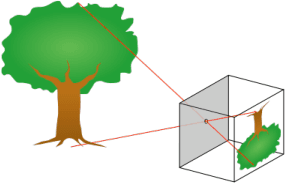
We provide criteria for deciding whether a given planar curve is an image of a given spatial curve, obtained by a central or a parallel projection with unknown parameters. These criteria reduce the projection problem to a certain modification of the equivalence problem of planar curves under affine and projective transformations. The latter problem can be addressed using Cartan's moving frame method. This leads to a novel algorithmic solution of the projection problem for curves. The computational advantage of the algorithms presented here, in comparison to algorithms based on a straightforward solution, lies in a significant reduction of a number of real parameters that has to be eliminated in order to establish existence or non-existence of a projection that maps a given spatial curve to a given planar curve. The same approach can be used to decide whether a given finite set of ordered points on a plane is an image of a given finite set of ordered points in R^3. The motivation comes from the problem of establishing a correspondence between an object and an image, taken by a camera with unknown position and parameters.