Euclidean and Affine Curve Reconstruction

We consider practical aspects of reconstructing planar curves with prescribed Euclidean or affine curvatures. These curvatures are invariant under the special Euclidean group and the equi-affine groups, respectively, and play an important role in computer vision and shape analysis. We discuss and implement algorithms for such reconstruction, and give estimates on how close reconstructed curves are relative to the closeness of their curvatures in appropriate metrics. Several illustrative examples are provided.

Non-congruent non-degenerate curves with identical signatures

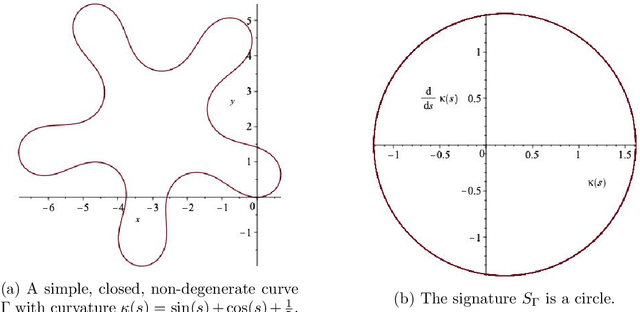
We construct examples of non-congruent, non-degenerate simple planar closed curves with identical Euclidean signatures, thus disproving a claim made in Hickman (J. Math Imaging Vis. 43:206-213, 2012) that all such curves must be congruent. Our examples include closed $C^\infty$ curves of the same length and the same symmetry group. We show a general mechanism for constructing such examples by exploiting the self-intersection points of the signature. We state an updated congruence criterion for simple closed non-degenerate curves and confirm that for curves with simple signatures the claim made by Hickman holds.