Non-congruent non-degenerate curves with identical signatures

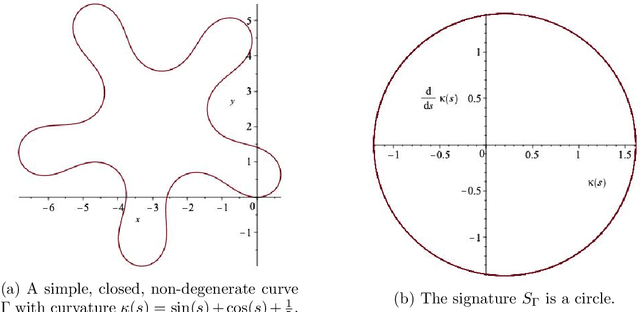
We construct examples of non-congruent, non-degenerate simple planar closed curves with identical Euclidean signatures, thus disproving a claim made in Hickman (J. Math Imaging Vis. 43:206-213, 2012) that all such curves must be congruent. Our examples include closed $C^\infty$ curves of the same length and the same symmetry group. We show a general mechanism for constructing such examples by exploiting the self-intersection points of the signature. We state an updated congruence criterion for simple closed non-degenerate curves and confirm that for curves with simple signatures the claim made by Hickman holds.