Object-image correspondence for curves under finite and affine cameras
Paper and Code
Feb 28, 2011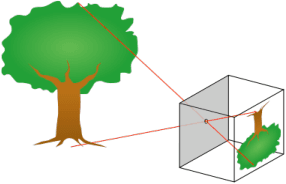

We provide criteria for deciding whether a given planar curve is an image of a given spatial curve, obtained by a central or a parallel projection with unknown parameters. These criteria reduce the projection problem to a certain modification of the equivalence problem of planar curves under affine and projective transformations. The latter problem can be addressed using Cartan's moving frame method. This leads to a novel algorithmic solution of the projection problem for curves. The computational advantage of the algorithms presented here, in comparison to algorithms based on a straightforward solution, lies in a significant reduction of a number of real parameters that has to be eliminated in order to establish existence or non-existence of a projection that maps a given spatial curve to a given planar curve. The same approach can be used to decide whether a given finite set of ordered points on a plane is an image of a given finite set of ordered points in R^3. The motivation comes from the problem of establishing a correspondence between an object and an image, taken by a camera with unknown position and parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge