Irene Gottlob
OCT segmentation: Integrating open parametric contour model of the retinal layers and shape constraint to the Mumford-Shah functional
Aug 08, 2018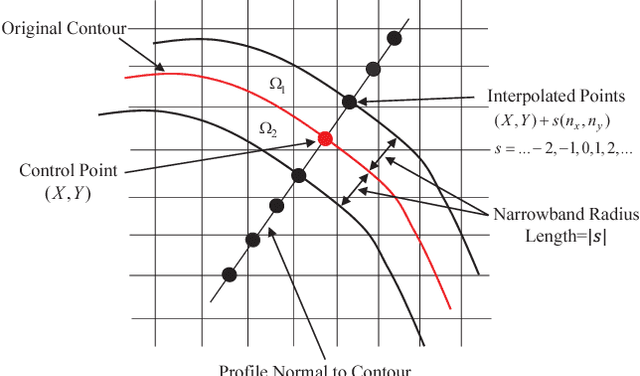

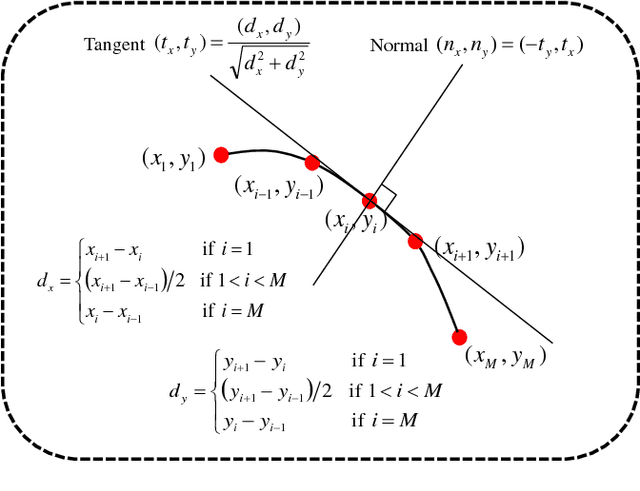
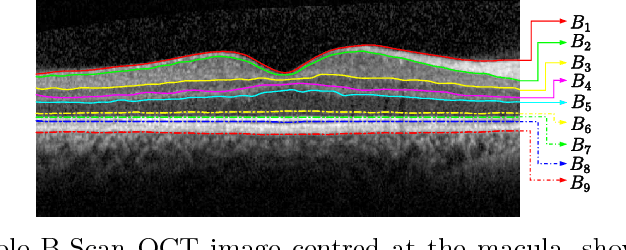
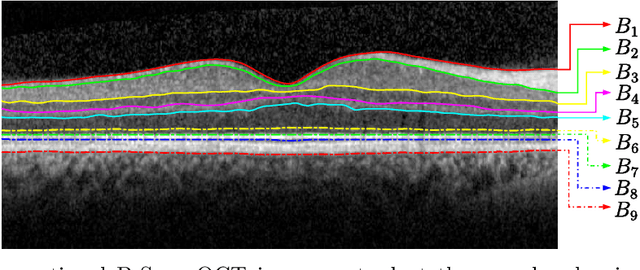
Abstract:In this paper, we propose a novel retinal layer boundary model for segmentation of optical coherence tomography (OCT) images. The retinal layer boundary model consists of 9 open parametric contours representing the 9 retinal layers in OCT images. An intensity-based Mumford-Shah (MS) variational functional is first defined to evolve the retinal layer boundary model to segment the 9 layers simultaneously. By making use of the normals of open parametric contours, we construct equal sized adjacent narrowbands that are divided by each contour. Regional information in each narrowband can thus be integrated into the MS energy functional such that its optimisation is robust against different initialisations. A statistical prior is also imposed on the shape of the segmented parametric contours for the functional. As such, by minimising the MS energy functional the parametric contours can be driven towards the true boundaries of retinal layers, while the similarity of the contours with respect to training OCT shapes is preserved. Experimental results on real OCT images demonstrate that the method is accurate and robust to low quality OCT images with low contrast and high-level speckle noise, and it outperforms the recent geodesic distance based method for segmenting 9 layers of the retina in OCT images.
Automated Segmentation of Retinal Layers from Optical Coherent Tomography Images Using Geodesic Distance
Sep 07, 2016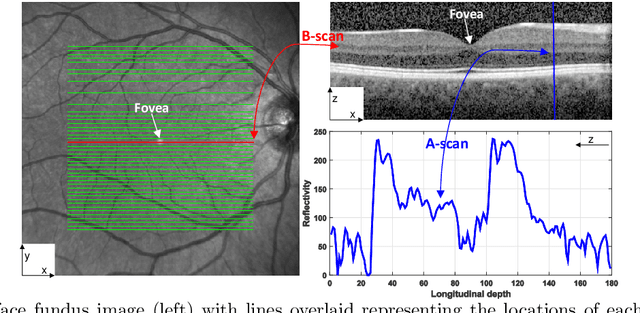


Abstract:Optical coherence tomography (OCT) is a non-invasive imaging technique that can produce images of the eye at the microscopic level. OCT image segmentation to localise retinal layer boundaries is a fundamental procedure for diagnosing and monitoring the progression of retinal and optical nerve disorders. In this paper, we introduce a novel and accurate geodesic distance method (GDM) for OCT segmentation of both healthy and pathological images in either two- or three-dimensional spaces. The method uses a weighted geodesic distance by an exponential function, taking into account both horizontal and vertical intensity variations. The weighted geodesic distance is efficiently calculated from an Eikonal equation via the fast sweeping method. The segmentation is then realised by solving an ordinary differential equation with the geodesic distance. The results of the GDM are compared with manually segmented retinal layer boundaries/surfaces. Extensive experiments demonstrate that the proposed GDM is robust to complex retinal structures with large curvatures and irregularities and it outperforms the parametric active contour algorithm as well as the graph theoretic based approaches for delineating the retinal layers in both healthy and pathological images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge